题目内容
设实数x、y满足y+x2=0,0＜a＜1,求证：loga(ax+ay)＜
+loga2.
证明:∵ax＞0,ay＞0,?
∴ax+ay≥2=2
.?
∵x-x2=x(1-x)≤［
］2=
,?
又0＜a＜1,?
∴a
≥a
，当x=
时，等号成立，但当x=
时，ax≠a
.?
∴ax+ay＞2a
.又0＜a＜1,?
∴loga(ax+ay)＜loga(
),?
即loga(ax+ay)＜loga2+
.
点评:由于0＜a＜1,只需证ax+ay≥
,?
∵ax+ay≥2
,?
只需证x+y≤
,x-x2≤
4.?
注意等号不同时成立，问题可解.借助分析法探路，然后利用综合法证明，若盲目用综合法推进，容易受阻.
练习册系列答案
相关题目
；
．
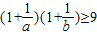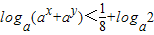