题目内容
已知函数f(x)=x2+2x+alnx.(1)求函数f(x)在点(1,f(1))处的切线方程;
(2)若函数f(x)在区间(0,2]上恒为单调函数,求实数a的取值范围;
(3)当t≥1时,不等式f(3t-2)≥3f(t)-6恒成立,求实数a的取值范围.
【答案】分析:(1)由求导公式和法则求出导数,求出f′(1)和f(1),代入点斜式方程,并化为一般式方程;
(2)根据题意和导数与单调性关系得,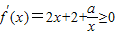 和
和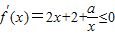 在(0,2]恒成立,再分离出常数a,再由二次函数的单调性求出“2x2+2x”在(0,2]上的最小值即可;
在(0,2]恒成立,再分离出常数a,再由二次函数的单调性求出“2x2+2x”在(0,2]上的最小值即可;
(3)由题意构造函数h(t)=f(3t-2)-[3f(t)-6],再求出导数并化简,根据t的范围,判断出一部分因式的符号,再对a分类讨论,判断出函数h(t)的单调性,求出函数h(t)的值域,再对照不等式看是否符合,求出a的范围.
解答:解:(1)由题意得,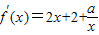 ,
,
∴f′(1)=4+a,且f(1)=3,
∴过点(1,f(1))的切线方程为y-3=(4+a)(x-1),
即(4+a)x-y-a-1=0,
(2)由f(x)在区间(0,2]上恒为单调函数得,
当f(x)在区间(0,2]上恒为单调增时,
∴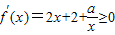 在(0,2]恒成立,
在(0,2]恒成立,
即2x2+2x+a≥0,∴-a≤2x2+2x,
∵2x2+2x在(0,2]上最小值为0,
∴-a≤0,即a≥0,
当f(x)在区间(0,2]上恒为单调减时,
∴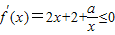 在(0,2]恒成立,
在(0,2]恒成立,
即2x2+2x+a≤0,∴-a≥2x2+2x,
∵2x2+2x在(0,2]上最小值为12,
∴-a≥12,即a≤-12.
综上得,实数a的取值范围是a≥0或a≤-12.
(3)由题意令:h(t)=f(3t-2)-[3f(t)-6](t≥1),
又∵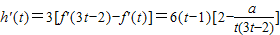 (t≥1),
(t≥1),
∵t≥1,∴t(3t-2)≥1.
1°当a≤2时,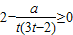 ,h′(t)≥0(等号不恒成立),
,h′(t)≥0(等号不恒成立),
∴h(t)在[1,+∞)上为增函数,
且h(1)=f(1)-[3f(1)-6]=3-3=0,
则h(t)≥h(1)对任意的t∈[1,+∞)恒成立.
2°当a>2时,
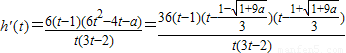 ,
,
∵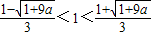 ,
,
∴当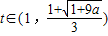 时,h′(t)<0,
时,h′(t)<0,
h(t)在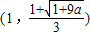 上为减函数,
上为减函数,
则h(t)<h(1)=0,不合题意,舍去.
综上所述,实数a的取值范围为(-∞,2].
点评:本题考查了导数的几何意义,导数与函数的单调性、最值,以及恒成立问题,考查了转化思想、分类讨论思想,构造函数法,综合性较强,难度很大.
(2)根据题意和导数与单调性关系得,
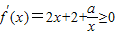 和
和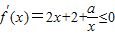 在(0,2]恒成立,再分离出常数a,再由二次函数的单调性求出“2x2+2x”在(0,2]上的最小值即可;
在(0,2]恒成立,再分离出常数a,再由二次函数的单调性求出“2x2+2x”在(0,2]上的最小值即可;(3)由题意构造函数h(t)=f(3t-2)-[3f(t)-6],再求出导数并化简,根据t的范围,判断出一部分因式的符号,再对a分类讨论,判断出函数h(t)的单调性,求出函数h(t)的值域,再对照不等式看是否符合,求出a的范围.
解答:解:(1)由题意得,
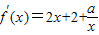 ,
,∴f′(1)=4+a,且f(1)=3,
∴过点(1,f(1))的切线方程为y-3=(4+a)(x-1),
即(4+a)x-y-a-1=0,
(2)由f(x)在区间(0,2]上恒为单调函数得,
当f(x)在区间(0,2]上恒为单调增时,
∴
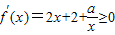 在(0,2]恒成立,
在(0,2]恒成立,即2x2+2x+a≥0,∴-a≤2x2+2x,
∵2x2+2x在(0,2]上最小值为0,
∴-a≤0,即a≥0,
当f(x)在区间(0,2]上恒为单调减时,
∴
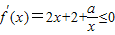 在(0,2]恒成立,
在(0,2]恒成立,即2x2+2x+a≤0,∴-a≥2x2+2x,
∵2x2+2x在(0,2]上最小值为12,
∴-a≥12,即a≤-12.
综上得,实数a的取值范围是a≥0或a≤-12.
(3)由题意令:h(t)=f(3t-2)-[3f(t)-6](t≥1),
又∵
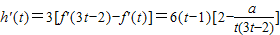 (t≥1),
(t≥1),∵t≥1,∴t(3t-2)≥1.
1°当a≤2时,
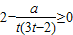 ,h′(t)≥0(等号不恒成立),
,h′(t)≥0(等号不恒成立),∴h(t)在[1,+∞)上为增函数,
且h(1)=f(1)-[3f(1)-6]=3-3=0,
则h(t)≥h(1)对任意的t∈[1,+∞)恒成立.
2°当a>2时,
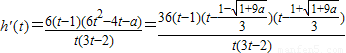 ,
,∵
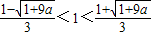 ,
,∴当
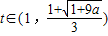 时,h′(t)<0,
时,h′(t)<0,h(t)在
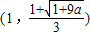 上为减函数,
上为减函数,则h(t)<h(1)=0,不合题意,舍去.
综上所述,实数a的取值范围为(-∞,2].
点评:本题考查了导数的几何意义,导数与函数的单调性、最值,以及恒成立问题,考查了转化思想、分类讨论思想,构造函数法,综合性较强,难度很大.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|