Question

已知F为抛物线C：y=x²的焦点，A（x₁，y₁），B（x₂，y₂）是抛物线C上的两点，且x₁＜x₂．
（1）若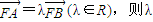为何值时，直线AB与抛物线C所围成的图形的面积最小？该面积的最小值是多少？
（2）若直线AB与抛物线C所围成的面积为，求线段AB的中点M的轨迹方程．

Answer 1

【答案】分析：（1）由题知，先写出抛物线C的焦点坐标，利用题中向量条件得出A，B两点坐标的关系式，从而写出直线AB的方程为，再利用定积分求出直线AB与抛物线C所围的面积的表达式，最后利用基本不等式求其最小值即可；
（2）先由题知A（x₁，x₁²），B（x₂，x₂²），且x₁＜x₂，写出直线AB的方程为y-x₁²=k（x-x₁），即y=（x₁+x₂）x-x₁x₂，再利用定积分求出直线AB与抛物线C所围的面积得到关于x₁，
x₂的方程，最终消去x₁，x₂得出点M的轨迹方程．
解答：解：（1）由题知，抛物线C的焦点．
因为共线，即
，
．
因为x₁＜x₂，所以x₁x₂=-．（2分）
由题设条件x₁＜x₂知，直线AB的斜率k一定存在，且
k=．（3分）
设直线AB的方程为y=kx+，则直线AB与抛物线C所围的面积
S=
=
=-
=
=
=

=，
当且仅当k=0，即x₁=-x₂，即λ=-1时，S_min=．（5分）
（2）由题知A（x₁，x₁²），B（x₂，x₂²），且x₁＜x₂，则直线AB的斜率k_AB=．
设直线AB的方程为y-x₁²=k（x-x₁），即y=（x₁+x₂）x-x₁x₂，
则直线AB与抛物线C所围的面积
S=
=，
因为S==2．（8分）设M（x，y），则x=+1，
y=+1，
所以y=x²+1．
故点M的轨迹方程为y=x²+1．（10分）
点评：本小题主要考查定积分在求面积中的应用、直线与圆锥曲线的综合问题、基本不等式等基础知识，考查运算求解能力，考查化归与转化思想．属于基础题．