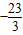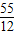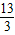题目内容
已知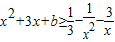
（x∈R且x≠0）恒成立，则b的最小值为（ ）A．
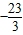
B．
C．
D．
【答案】分析：已知
，通过转化可得b≥-x2-3x
，再利用均值不等式进行放缩，从而求出b的最小值；
解答：解：∵
（x∈R且x≠0）恒成立，
可得b≥-x2-3x
，（x∈R且x≠0）恒成立，
求出-x2-3x
的最大值，
∵-x2-
=-（x2+
）≤-2，（x=1时等号成立）；
-3x-
=-3（x+
）≤-6（x=1时等号成立）；
∴-x2-3x
≤-2-6+
=-
；
∴b≥-
，
故选A；
点评：此题考查函数的恒成立问题及均值不等式的应用，解题的过程中用到了转化的思想，是一道基础题；
，通过转化可得b≥-x2-3x，再利用均值不等式进行放缩，从而求出b的最小值；解答：解：∵
（x∈R且x≠0）恒成立，可得b≥-x2-3x
，（x∈R且x≠0）恒成立，求出-x2-3x
的最大值，∵-x2-
=-（x2+）≤-2，（x=1时等号成立）；-3x-
=-3（x+）≤-6（x=1时等号成立）；∴-x2-3x
≤-2-6+=-；∴b≥-
，故选A；
点评：此题考查函数的恒成立问题及均值不等式的应用，解题的过程中用到了转化的思想，是一道基础题；
练习册系列答案
相关题目
)=cx(a、b、c∈R,ab≠0,a2≠b2),求f(x);
x2,其中x是产品售出的数量，且0≤x≤500.若x为年产量，y表示利润，求y=f(x)的解析式.
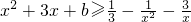（x∈R且x≠0）恒成立，则b的最小值为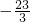
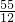
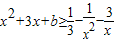（x∈R且x≠0）恒成立，则b的最小值为（ ）
