题目内容
已知向量 ,满足
,满足 ,
,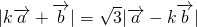 ,k>0,
,k>0,
(1)用k表示 ,并求
,并求 与
与 的夹角θ的最大值;
的夹角θ的最大值;
(2)如果 ,求实数k的值.
,求实数k的值.
解:(1)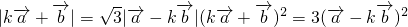
即∴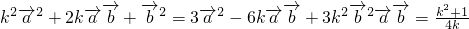 .
.
∵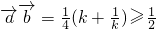 ,.
,.
此时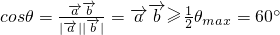 .
.
(2)∵ ,∴
,∴ 与
与 夹角为0°或180°
夹角为0°或180°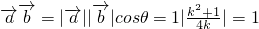
又∵k>0,∴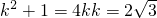 .
.
分析:(1)利用向量的模的平方等于向量的平方,利用向量的运算律表示出 ;利用基本不等式求出数量积的取值范围,
;利用基本不等式求出数量积的取值范围,
利用向量的数量积公式表示出夹角余弦,求出夹角范围.
(2)根据向量共线的夹角是0°或180°,利用向量的数量积公式列出等式求出k值.
点评:本题考查向量的模的平方等于向量的平方;向量的数量积公式表示向量的夹角;向量共线的充要条件.
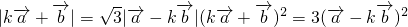
即∴
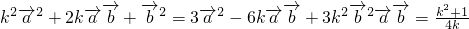 .
.∵
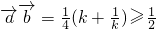 ,.
,.此时
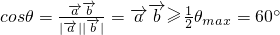 .
.(2)∵
 ,∴
,∴ 与
与 夹角为0°或180°
夹角为0°或180°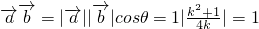
又∵k>0,∴
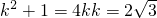 .
.分析:(1)利用向量的模的平方等于向量的平方,利用向量的运算律表示出
 ;利用基本不等式求出数量积的取值范围,
;利用基本不等式求出数量积的取值范围,利用向量的数量积公式表示出夹角余弦,求出夹角范围.
(2)根据向量共线的夹角是0°或180°,利用向量的数量积公式列出等式求出k值.
点评:本题考查向量的模的平方等于向量的平方;向量的数量积公式表示向量的夹角;向量共线的充要条件.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 ,满足
,满足 ,
, .
. 的坐标,以及向量
的坐标,以及向量 与
与 的夹角;
的夹角; 与
与 垂直,求实数k的值.
垂直,求实数k的值. ,满足
,满足 ,
, ,k>0,
,k>0, ,并求
,并求 与
与 的夹角θ的最大值;
的夹角θ的最大值; ,求实数k的值.
,求实数k的值. ,
, 满足:
满足: ,且
,且 (k>0).则向量
(k>0).则向量 与向量
与向量 的夹角的最大值为( )
的夹角的最大值为( )



 ,满足
,满足 ,
, ,
, 。
。 ,并求
,并求 与
与 的夹角
的夹角 的最大值;
的最大值; ,求实数k的值。
,求实数k的值。