题目内容
已知向量 ,满足
,满足 ,
, .
.(1)求向量
 的坐标,以及向量
的坐标,以及向量 与
与 的夹角;
的夹角;(2)若向量
 与
与 垂直,求实数k的值.
垂直,求实数k的值.
【答案】分析:(1)求出  的坐标,设
的坐标,设  与
与  的夹角为 θ,则由 cos<
的夹角为 θ,则由 cos< ,
, >=
>= 求出 θ 的值.
求出 θ 的值.
(2)根据题意,求出两个向量的差的坐标,利用向量垂直的充要条件:数量积为0列出方程,求出k的值.
解答:解:(1) =(3,1),设
=(3,1),设  与
与  的夹角为 θ,
的夹角为 θ,
则 cos< ,
, >=
>= =
= =
= .
.
根据题意得 0≤θ≤π,∴θ= .
.
(2): =(3,1),
=(3,1),
∵向量 与
与 垂直
垂直
∴3×(k-2)+2k+1=0
解得k=1.
点评:本题考查两个向量的数量积的定义,两个向量的数量积公式,两个向量坐标形式的运算,向量的模的定义和求法,函数的单调性的应用,准确运算是解题的关键.
 的坐标,设
的坐标,设  与
与  的夹角为 θ,则由 cos<
的夹角为 θ,则由 cos< ,
, >=
>= 求出 θ 的值.
求出 θ 的值.(2)根据题意,求出两个向量的差的坐标,利用向量垂直的充要条件:数量积为0列出方程,求出k的值.
解答:解:(1)
 =(3,1),设
=(3,1),设  与
与  的夹角为 θ,
的夹角为 θ,则 cos<
 ,
, >=
>= =
= =
= .
.根据题意得 0≤θ≤π,∴θ=
 .
.(2):
 =(3,1),
=(3,1),
∵向量
 与
与 垂直
垂直∴3×(k-2)+2k+1=0
解得k=1.
点评:本题考查两个向量的数量积的定义,两个向量的数量积公式,两个向量坐标形式的运算,向量的模的定义和求法,函数的单调性的应用,准确运算是解题的关键.

练习册系列答案
相关题目
 、
、 满足
满足 ,则
,则 .
. ,实数
,实数 满足
满足 ,则
,则 的最小值为( )
的最小值为( ) B.1 C.
B.1 C. D.
D.
 ,
, 满足
满足 ,
, ,
, ,则
,则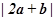 的值为_______.
的值为_______.