题目内容
设函数f(x)=|lgx|,若0<a<b,且f(a)>f(b),证明:ab<1。
证明:由已知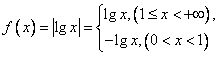 ,
,
∵0<a<b,f(a)>f(b),
∴a、b不能同时在区间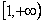 上,
上,
又由于0<a<b,故必有a∈(0,1);
若b∈(0,1),显然有ab<1;
若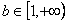 ,由f(a)-f(b)>0,
,由f(a)-f(b)>0,
有-lga-lgb>0,故lgab<0,
∴ab<1。
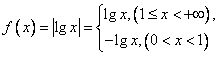 ,
,∵0<a<b,f(a)>f(b),
∴a、b不能同时在区间
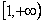 上,
上,又由于0<a<b,故必有a∈(0,1);
若b∈(0,1),显然有ab<1;
若
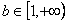 ,由f(a)-f(b)>0,
,由f(a)-f(b)>0,有-lga-lgb>0,故lgab<0,
∴ab<1。

练习册系列答案
相关题目
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)