题目内容

函数f（x）=sin（2x-
π
3
）的对称中心为
 
．
考点：正弦函数的图象
专题：三角函数的图像与性质
分析：根据正弦函数的图象和性质即可得到结论．
解答： 解：由2x-
π
3
=kπ，解得x=
π
6
+
kπ
2
，k∈Z，
故函数的对称中心为（
π
6
+
kπ
2
，0），k∈Z，
故答案为：（
π
6
+
kπ
2
，0），k∈Z
点评：本题主要考查三角函数的对称中心的求解，要求熟练掌握正弦函数的图象和性质．
练习册系列答案
相关题目
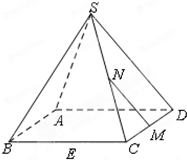某企业2010年的利润是1200万元，计划从2011年起每年比上一年利润增加200万元，若经过x年累计利润为y万元，试写出y是x的函数关系式．
如图，在正四棱锥S-ABCD中，E，M，N分别是BC，CD，SC的中点，动点P在线段MN上运动时，下列四个结论：①EP⊥AC1；②EP∥BD；③EP∥面SBD；④EP⊥面SAC．中恒成立的为（　　）
A、①③B、③④C、①②D、②③④
已知偶函数f（x），满足f（x+2）=
1
f(x)
，若f（-2）=1，则f（2014）=
 
．
已知函数f（x）=2sin（2x-
π
6
），则如下结论：
①函数f（x）的最小正周期为π；
②函数f（x）在[
π
6
，
5π
12
]上的值域为[1，
3
]；
③函数f（x）在（
π
3
，
7π
12
）上是减函数；
④函数y=f（x）的图象向左平移
π
6
个单位得到函数y=2sin2x的图象，
其中正确的是
 
（写出所有正确的序号）
已知定义在区间（-1，1）上的函数f（x）=
ax+b
1+x2
是奇函数，且f（
1
2
）=
2
5
，
（1）确定f（x）的解析式；
（2）判断f（x）的单调性并用定义证明；
（3）解不等式f（t-1）+f（t）＜0．
从集合A={1，2，3}和B={1，4，5，6}中各取一个元素作为点的坐标，则在直角坐标系中能确定不同点的个数是
 
 个．
已知函数y=f（x）是R上的偶函数，对于x∈R都有f（x+4）=f（x）+f（2）成立，且f（-3）=-2，当x1，x2∈[0，2]且x1≠x2时，都有
f(x1)-f(x2)
x1-x2
＞0，则给出下列命题：
①函数y=f（x）图象的一条对称轴为x=2；      
②f（2011）=-2；
③函数y=f（x）在[-6，-4]上为减函数；      
④方程f（x）=0 在[-6，6]上有4个根，
上述命题中的所有正确命题的序号是
 
．
16
81
的平方根是
 
，
64
的立方根是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网