Question

下列命题中，其中真命题的个数有（ ）个
①若f（x）是定义在[-1，1]上的偶函数，且在[-1，0]上是增函数，，则f（sinθ）＞f（cosθ）
②△ABC为锐角三角形是tanA+tanB+tanC＞0的充要条件
③若||=||，
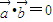
④函数是其对称中心
⑤命题P：?x∈R，mx²+1≤0，命题q：?x∈R，x²+mx+1＞0，若p∨q为假命题，则实数m的取值范围是m＞2．
A．1
B．2
C．3
D．4

Answer 1

【答案】分析：根据函数奇偶性与单调性的综合应用，可以判断①的真假；由三角形内角的三角函数的性质，可判断②的真假；同平面向量的性质可判断③的真假；由函数的对称性能判断④的真假；由复合命题的真假判断能得到⑤的真假．
解答：解：①若f（x）是定义在[-1，1]上的偶函数，且在[-1，0]上是增函数，
则函数在[0，1]上为减函数，
若，则0＜cosθ＜sinθ＜1，
则f（sinθ）＜f（cosθ），故①为假命题；
②∵tanA+tanB=tan（A+B）（1-tanAtanB）
∴tanA+tanB+tanC=tan（A+B）（1-tanAtanB）+tanC=tanC（tanAtanB-1）+tanC=tanAtanBtanC＞0，
∴A，B，C是△ABC的内角，故内角都是锐角．
反之，当△ABC的内角都是锐角时，tanA+tanB+tanC＞0．
故△ABC为锐角三角形是tanA+tanB+tanC＞0的充要条件，故②是真命题；
③∵||=||，∴=，
∴，故③正确；
④设f（x）的对称中心是（a，b），有f（x）+f（2a-x）=2b
f（x）+f（2a-x）=+
=（4x²-8ax+2a+2）÷（4x²-8ax-4a-1）
=2b，
∴2a+2+4a+1=0，2b=1
a=-，b=，
∴f（x）的对称中心是（-，），故④不正确；
⑤∵p∨q为假命题，∴p，q均为假命题，
即￢p：x∈R，mx²+1＞0和￢q：x∈R，x²+mx+1≤0均为真命题，
由￢p：x∈R，mx²+1＞0为真命题，得到m≥0；
由￢q：x∈R，x²+mx+1≤0为真命题，得到△=m²-4≥0，解得m≥2，或m≤-2．
综上，m≥2．故⑤正确．
故选C．
点评：本题考查命题的真假判断，是基础题．解题时要认真审题，注意函数的性质、三角形内角三角函数的性质、平面向量等知识点的合理运用．