��Ŀ����
���������У�����������ĸ����У���������
����f��x���Ƕ�����[-1��1]�ϵ�ż����������[-1��0]�������������ȡ�(
��
)����f��sin�ȣ���f��cos�ȣ�
�ڡ�ABCΪ�����������tanA+tanB+tanC��0�ij�Ҫ����
����|
+
|=|
-
|��
•
=0
�ܺ���f(x)=
��(-
��-
)����Գ�����
������P��?x��R��mx2+1��0������q��?x��R��x2+mx+1��0����p��qΪ�����⣬��ʵ��m��ȡֵ��Χ��m��2��
����f��x���Ƕ�����[-1��1]�ϵ�ż����������[-1��0]�������������ȡ�(
| �� |
| 4 |
| �� |
| 2 |
�ڡ�ABCΪ�����������tanA+tanB+tanC��0�ij�Ҫ����
����|
| a |
| b |
| a |
| b |
| a |
| b |
�ܺ���f(x)=
| x-1 |
| 2x+1 |
| 1 |
| 2 |
| 1 |
| 2 |
������P��?x��R��mx2+1��0������q��?x��R��x2+mx+1��0����p��qΪ�����⣬��ʵ��m��ȡֵ��Χ��m��2��
���������ݺ�����ż���뵥���Ե��ۺ�Ӧ�ã������жϢٵ���٣����������ڽǵ����Ǻ��������ʣ����жϢڵ���٣�ͬƽ�����������ʿ��жϢ۵���٣��ɺ����ĶԳ������жϢܵ���٣��ɸ������������ж��ܵõ��ݵ���٣�
����⣺����f��x���Ƕ�����[-1��1]�ϵ�ż����������[-1��0]������������
������[0��1]����������
���ȡ�(
��
)����0��cos�ȣ�sin�ȣ�1��
��f��sin�ȣ���f��cos�ȣ����ʢ�Ϊ�����⣻
�ڡ�tanA+tanB=tan��A+B����1-tanAtanB��
��tanA+tanB+tanC=tan��A+B����1-tanAtanB��+tanC=tanC��tanAtanB-1��+tanC=tanAtanBtanC��0��
��A��B��C�ǡ�ABC���ڽǣ����ڽǶ�����ǣ�
��֮������ABC���ڽǶ������ʱ��tanA+tanB+tanC��0��
�ʡ�ABCΪ�����������tanA+tanB+tanC��0�ij�Ҫ�������ʢ��������⣻
�ۡ�|
+
|=|
-
|����
2+
•
+
2=
2-
•
+
2��
��
•
=0���ʢ���ȷ��
����f��x���ĶԳ������ǣ�a��b������f��x��+f��2a-x��=2b
f��x��+f��2a-x��=
+
=��4x2-8ax+2a+2���£�4x2-8ax-4a-1��
=2b��
��2a+2+4a+1=0��2b=1
a=-
��b=
��
��f��x���ĶԳ������ǣ�-
��
�����ʢܲ���ȷ��
�ݡ�p��qΪ�����⣬��p��q��Ϊ�����⣬
���Vp��x��R��mx2+1��0�ͩVq��x��R��x2+mx+1��0��Ϊ�����⣬
�ɩVp��x��R��mx2+1��0Ϊ�����⣬�õ�m��0��
�ɩVq��x��R��x2+mx+1��0Ϊ�����⣬�õ���=m2-4��0�����m��2����m��-2��
���ϣ�m��2���ʢ���ȷ��
��ѡC��
������[0��1]����������
���ȡ�(
| �� |
| 4 |
| �� |
| 2 |
��f��sin�ȣ���f��cos�ȣ����ʢ�Ϊ�����⣻
�ڡ�tanA+tanB=tan��A+B����1-tanAtanB��
��tanA+tanB+tanC=tan��A+B����1-tanAtanB��+tanC=tanC��tanAtanB-1��+tanC=tanAtanBtanC��0��
��A��B��C�ǡ�ABC���ڽǣ����ڽǶ�����ǣ�
��֮������ABC���ڽǶ������ʱ��tanA+tanB+tanC��0��
�ʡ�ABCΪ�����������tanA+tanB+tanC��0�ij�Ҫ�������ʢ��������⣻
�ۡ�|
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| b |
| a |
| a |
| b |
| b |
��
| a |
| b |
����f��x���ĶԳ������ǣ�a��b������f��x��+f��2a-x��=2b
f��x��+f��2a-x��=
| x-1 |
| 2x+1 |
| 2a-x-1 |
| 4a-2x+1 |
=��4x2-8ax+2a+2���£�4x2-8ax-4a-1��
=2b��
��2a+2+4a+1=0��2b=1
a=-
| 1 |
| 2 |
| 1 |
| 2 |
��f��x���ĶԳ������ǣ�-
| 1 |
| 2 |
| 1 |
| 2 |
�ݡ�p��qΪ�����⣬��p��q��Ϊ�����⣬
���Vp��x��R��mx2+1��0�ͩVq��x��R��x2+mx+1��0��Ϊ�����⣬
�ɩVp��x��R��mx2+1��0Ϊ�����⣬�õ�m��0��
�ɩVq��x��R��x2+mx+1��0Ϊ�����⣬�õ���=m2-4��0�����m��2����m��-2��
���ϣ�m��2���ʢ���ȷ��
��ѡC��
���������⿼�����������жϣ��ǻ����⣮����ʱҪ�������⣬ע�⺯�������ʡ��������ڽ����Ǻ��������ʡ�ƽ��������֪ʶ��ĺ������ã�

��ϰ��ϵ�д�
 ��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
�����Ŀ
 ����f��sin�ȣ���f��cos�ȣ�
����f��sin�ȣ���f��cos�ȣ� |=|
|=| |��
|��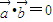
 ����Գ�����
����Գ�����