题目内容
在四棱锥 中,
中, ,
, 平面
平面 ,
, 为
为 的中点,
的中点, ,
, .
.
(Ⅰ)求四棱锥 的体积
的体积 ;
;
(Ⅱ)若 为
为 的中点,求证:平面
的中点,求证:平面 平面
平面 .
.
(Ⅰ)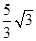 (Ⅱ)见解析
(Ⅱ)见解析
解析试题分析:(Ⅰ)由 平面
平面 知PA是棱锥P—ABCD的高,在Rt△ABC中,由AB=1,∠BAC=60o求出BC、BC,从而求出△ABC的面积,同理求出△ACD的面积,即可计算出四边形ABCD的面积,代入棱锥体积公式求出棱锥P—ABCD的体积;(Ⅱ)由由
知PA是棱锥P—ABCD的高,在Rt△ABC中,由AB=1,∠BAC=60o求出BC、BC,从而求出△ABC的面积,同理求出△ACD的面积,即可计算出四边形ABCD的面积,代入棱锥体积公式求出棱锥P—ABCD的体积;(Ⅱ)由由 平面
平面 知,PA⊥CD,由CD⊥AC,知CD⊥面PAC,因为E、F分别为PD、PC的中点,所以EF∥CD,由线面垂直性质得EF⊥面PAC,因为EF在面PAC内,根据面面垂直判定定理得面PAC⊥面AEF.
知,PA⊥CD,由CD⊥AC,知CD⊥面PAC,因为E、F分别为PD、PC的中点,所以EF∥CD,由线面垂直性质得EF⊥面PAC,因为EF在面PAC内,根据面面垂直判定定理得面PAC⊥面AEF.
试题解析:(Ⅰ)在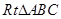 中,
中, ,
, ,
,
∴ 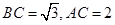 2分
2分
在 中,
中,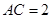 ,
,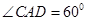 ,
,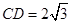 4分
4分
∵  ,
,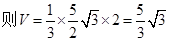 6分
6分
(Ⅱ)∵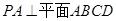 , ∴
, ∴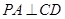 7分
7分
又 ,
,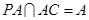
∴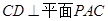 , 8分
, 8分
∵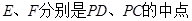 ,∴
,∴ //
//
∴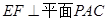 10分
10分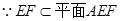 ,∴
,∴ 12分
12分
考点:棱锥的体积公式,线面垂直的判定与性质,面面垂直的判定,推理论证能力,运算求解能力

练习册系列答案
相关题目
 ,FC
,FC  平面ABCD, AE
平面ABCD, AE 
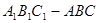 的三视图,主视图和侧视图是全等的矩形,俯视图是等腰直角三角形,点M是A1B1的中点。
的三视图,主视图和侧视图是全等的矩形,俯视图是等腰直角三角形,点M是A1B1的中点。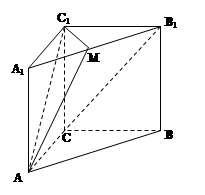

 ,且AC=BC.
,且AC=BC. 平面EBC;
平面EBC; 的大小.
的大小.


 为不重合的两条直线,
为不重合的两条直线, 为不重合的两个平面,给出下列命题:
为不重合的两个平面,给出下列命题: ∥
∥ 且
且 ∥
∥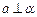 且
且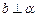 ,则
,则 ,则
,则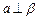 ,则
,则 中,
中,
 、
、 分别为棱
分别为棱 、
、 的中点,则点
的中点,则点 到平面
到平面 的距离为
的距离为  为互不重合的平面,W#W$W%.K**S*&5^U
为互不重合的平面,W#W$W%.K**S*&5^U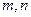 是互不重合的直线,给出下列四个命题:
是互不重合的直线,给出下列四个命题: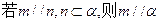
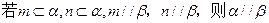
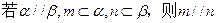
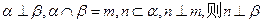 ;
;