题目内容
如图,边长为2的正方形ACDE所在的平面与平面ABC垂直,AD与CE的交点为M, ,且AC=BC.
,且AC=BC.
(1)求证: 平面EBC;
平面EBC;
(2)求二面角 的大小.
的大小.
(1)祥见解析;(2) .
.
解析试题分析:由已知四边形 是正方形,知其两条对角线互相垂直平分,且
是正方形,知其两条对角线互相垂直平分,且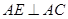 ,又因为平面
,又因为平面 平面
平面 ,
, 平面
平面 ,故可以以点
,故可以以点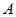 为原点,以过
为原点,以过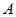 点平行于
点平行于 的直线为
的直线为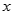 轴,分别以直线
轴,分别以直线 和
和 为
为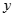 轴和
轴和 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系 ;又因为正方形ACDE的边长为2,且三角形ABC是以角C为直角的直角三角形,从而就可以写出点A,B,C,E及点M的空间直角坐标;则(1)求出向量
;又因为正方形ACDE的边长为2,且三角形ABC是以角C为直角的直角三角形,从而就可以写出点A,B,C,E及点M的空间直角坐标;则(1)求出向量 的坐标,从而可证
的坐标,从而可证 ,这样就可证明直线AM与平面EBC内的两条相交直线垂直,故得直线AM与平面EBC垂直;(2)由(1)知
,这样就可证明直线AM与平面EBC内的两条相交直线垂直,故得直线AM与平面EBC垂直;(2)由(1)知 是平面EBC的一个法向量,其坐标已求,再设平面EAB的一个法向量为
是平面EBC的一个法向量,其坐标已求,再设平面EAB的一个法向量为 ,则由
,则由 且
且 ,可求得平面EAB的一个法向量;从而可求出所求二面角的两个面的法向量夹角的余弦值,由图可知所求二面角为锐二面角,故二面角的余弦值等于两个面的法向量夹角余弦值的绝对值,从而就可求得所求二面角的大小.另本题也可用几何方法求解证明.
,可求得平面EAB的一个法向量;从而可求出所求二面角的两个面的法向量夹角的余弦值,由图可知所求二面角为锐二面角,故二面角的余弦值等于两个面的法向量夹角余弦值的绝对值,从而就可求得所求二面角的大小.另本题也可用几何方法求解证明.
试题解析:∵四边形 是正方形 ,
是正方形 , 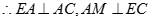 ,
,
∵平面 平面
平面 ,
, 平面
平面 ,
,
∴可以以点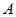 为原点,以过
为原点,以过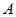 点平行于
点平行于 的直线为
的直线为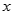 轴,
轴,
分别以直线 和
和 为
为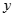 轴和
轴和 轴,建立如图所示的空间直角坐标系
轴,建立如图所示的空间直角坐标系 .
.
设 ,则
,则
 ,
, 是正方形
是正方形 的对角线的交点,
的对角线的交点, .
.
(1)
 ,
, ,
,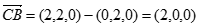 ,
, ,
, 
 平面
平面 .
.
(2) 设平面 的法向量为
的法向量为 ,则
,则 且
且 ,
, 且
且 .
.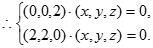 即
即
取 ,则
,则 , 则
, 则 .
.
又∵
练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 中,
中, ,
, 平面
平面 ,
, 为
为 的中点,
的中点, ,
, .
. ;
; 为
为 的中点,求证:平面
的中点,求证:平面 平面
平面 .
.
 为斜三棱柱
为斜三棱柱 的侧棱
的侧棱 上一点,
上一点,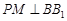 交
交 于点
于点 ,
, 交
交 于点
于点 .
.
 ;
; 中有余弦定理:
中有余弦定理: .
.
 -A BC中,AB
-A BC中,AB 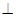 AC, AB=AC=2,
AC, AB=AC=2,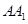 =4,点D是BC的中点.
=4,点D是BC的中点.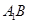 与
与 所成角的余弦值;
所成角的余弦值; 与
与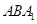 所成二面角的正弦值.
所成二面角的正弦值.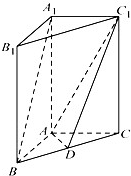
 ,BC=,求二面角S-AB-C的余弦值.
,BC=,求二面角S-AB-C的余弦值.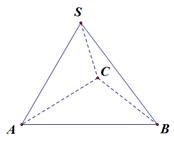
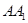 ,
, 为圆柱
为圆柱 的母线,
的母线, 是底面圆
是底面圆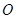 的直径,
的直径,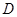 ,
,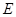 分别是
分别是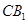 的中点,
的中点,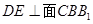 .
. ;
; ;
;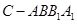 内会有被捕的危险,求鱼被捕的概率.
内会有被捕的危险,求鱼被捕的概率.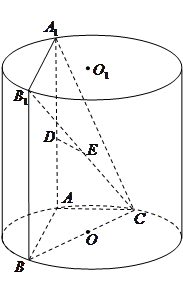
 与平面
与平面 相交,直线
相交,直线 是平面
是平面 ,则直线
,则直线