题目内容
【题目】一个简单几何体的三视图如图所示，其中正视图是一个正三角形，俯视图是等腰直角三角形，则该几何体的体积为 ， 表面积为 ．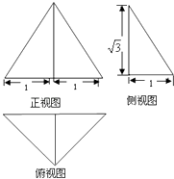 
【答案】
?；
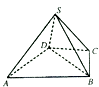
【解析】解：由三视图知：几何体是三棱锥，且几何体的后侧面SAC与底面垂直，高SO为 
， 如图：
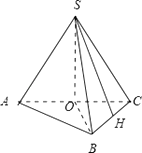
其中OA=OB=OC=1，SO⊥平面ABC，
AB=BC= 
，SA=SB=SC=2，
底面△ABC的面积为： 
，
后侧面△SAC的面积为： 
，
左右两个侧面△SAB和△SBC的底面边长为 ，两腰长为2，
故底边上的高为： 
= 
，
故左右两个侧面△SAB和△SBC的面积为： 
，
故几何体的表面积： ，
几何体的体积V= 
= ，
所以答案是： ，
【考点精析】根据题目的已知条件，利用由三视图求面积、体积的相关知识可以得到问题的答案，需要掌握求体积的关键是求出底面积和高；求全面积的关键是求出各个侧面的面积．
练习册系列答案
冲刺100分单元优化练考卷系列答案
相关题目
