题目内容
已知p:方程x2+mx+1=0有两个不等的负根;q:方程4x2+4(m-2)x+1=0无实根.若p或q为真,p且q为假,求m的取值范围.
思路解析:由“p且q为假、p或q为真”得p、q中有一真一假.可分两类进行讨论. 解:由已知p或q为真,p且q为假可得,p、q中一真一假.当p真q假时,即方程x2+mx+1=0有两个不等的负根成立,且方程4x2+4(m-2)x+1=0无实根不成立, m需满足 解得m≥3. 当p假q真时,即方程x2+mx+1=0有两个不等的负根不成立,且方程4x2+4(m-2)x+1=0无实根成立,m需满足 解得1<m≤2. 综上,满足条件的m的取值范围是m≥3,或1<m≤2. 深化升华 由复合命题真值表判断出p、q一真一假是解决本题的关键,其次求解过程中运用了补集思想.如q假时m的范围集合即为q真时m的范围集合的补集等.
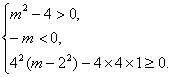
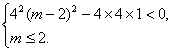
 练习册系列答案
练习册系列答案
中考说明与训练系列答案
中考备考每天一点系列答案
征服英语名师课时计划系列答案
考前系列答案
口算心算快速算系列答案
跨越中考总复习方略系列答案
新语文阅读训练系列答案
秒杀口算题系列答案

中考1加1系列答案
相关题目