题目内容
由曲线y=x2和直线x=0,x=1,y=t2,t∈(0,1)所围成的图形(阴影部分)的面积的最小值为( )
A. | B. | C.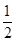 | D. |
A
解析试题分析:因为t∈(0,1),所以由 ,所以阴影部分的面积为
,所以阴影部分的面积为 =
= 。
。
考点:定积分。
点评:在平常做题中,很多同学认为面积就是定积分,定积分就是面积。从而导致此题出错。实际上,我们是用定积分来求面积,但并不等于定积分就是面积。

练习册系列答案
相关题目
若 ,则k=
,则k=
| A.1 | B.0 | C.0或1 | D.以上都不对 |
一物体在力 (
( 单位为
单位为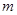 ,
, 单位为
单位为 )的作用下,沿着与力
)的作用下,沿着与力 相同的方向从
相同的方向从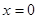 处运动到
处运动到 处,则力
处,则力 所作的功是:
所作的功是:
| A.40 | B.42 | C.48 | D.52 |
已知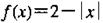 ,则
,则 = ( )
= ( )
| A.3 | B.4 | C.3.5 | D.4.5 |
已知曲线方程f(x)=sin2x+2ax(a∈R),若对任意实数m,直线l:x+y+m=0都不是曲线y=f(x)的切线,则a的取值范围是
A.(- ,-1)∪(-1,0) ,-1)∪(-1,0) | B.(- ,-1)∪(0,+ ,-1)∪(0,+ ) ) |
C.(-1,0)∪(0,+ ) ) | D.a∈R且a≠0,a≠-1 |
曲线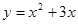 在点A(2,10)处的切线的斜率是
在点A(2,10)处的切线的斜率是
| A.4 | B.5 | C.6 | D.7 |
设函数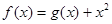 ,曲线
,曲线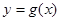 在点
在点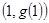 处的切线方程为
处的切线方程为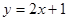 ,则曲线
,则曲线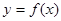 在点
在点 处的切线的斜率为( )
处的切线的斜率为( )
A.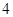 | B.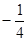 | C. | D.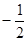 |
设f(x)、g(x)分别是定义在R上的奇函数和偶函数,当x<0时,f′(x)·g(x)+f(x)·g′(x)>0,且f(-3)·g(-3)=0,则不等式f(x)·g(x)<0的解集是( )
| A.(-3,0)∪(3,+∞) |
| B.(-3,0)∪ (0,3) |
| C.(-∞,-3)∪(3,+∞) |
| D.(-∞,-3)∪(0,3) |
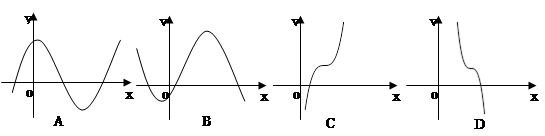
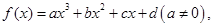 记
记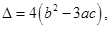 则当
则当 的大致图像为( )
的大致图像为( )