题目内容
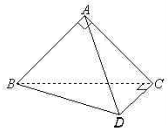 如图,△ABC与△BCD是一副三角板,它们所在的两个平面互相垂直,且AB=AC,∠BAC=∠BCD=90°,∠CBD=30°.
如图,△ABC与△BCD是一副三角板,它们所在的两个平面互相垂直,且AB=AC,∠BAC=∠BCD=90°,∠CBD=30°.(Ⅰ)求证:△ACD和△BAD都是直角三角形;
(Ⅱ)求直线BD与平面ACD所成角的正弦值.
分析:(Ⅰ)根据BC⊥CD,平面ABC⊥平面BCD,利用面面垂直的性质得DC⊥平面ABC,从而得到线线垂直,再利用线面垂直的判定得AB⊥平面ACD,从而证得结论;
(Ⅱ)由(Ⅰ)可知∠BDA为直线BD与平面ACD所成角.设出AB的长度,利用解三角形求解直线BD与平面ACD所成角的正弦值.
(Ⅱ)由(Ⅰ)可知∠BDA为直线BD与平面ACD所成角.设出AB的长度,利用解三角形求解直线BD与平面ACD所成角的正弦值.
解答: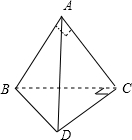 (Ⅰ)证明:如图,
(Ⅰ)证明:如图,
由已知,△ABC与△BCD是直角三角形,
又平面ABC⊥平面BCD,平面ABC∩平面BCD=BC,且CD⊥BC,
∴CD⊥平面ABC,又AC?平面ABC,AB?平面ABC,
∴CD⊥AC,CD⊥AB,△ACD是直角三角形.
又AB⊥AC,AC∩CD=C,∴AB⊥平面ACD,AD?ADC,∴AB⊥AD.
∴△ABD也是直角三角形.
∴△ACD和△BAD都是直角三角形;
(Ⅱ)由(Ⅰ)知,AB⊥平面ACD,∴∠BDA为直线BD与平面ACD所成角.
设AB=a,∵△ABC为等腰直角三角形,∴BC=
a,
在Rt△BCD中,∵∠CBD=30°,∴BD=
,
则sin∠BDA=
=
.
∴直线BD与平面ACD所成角的正弦值为
.
 (Ⅰ)证明:如图,
(Ⅰ)证明:如图,由已知,△ABC与△BCD是直角三角形,
又平面ABC⊥平面BCD,平面ABC∩平面BCD=BC,且CD⊥BC,
∴CD⊥平面ABC,又AC?平面ABC,AB?平面ABC,
∴CD⊥AC,CD⊥AB,△ACD是直角三角形.
又AB⊥AC,AC∩CD=C,∴AB⊥平面ACD,AD?ADC,∴AB⊥AD.
∴△ABD也是直角三角形.
∴△ACD和△BAD都是直角三角形;
(Ⅱ)由(Ⅰ)知,AB⊥平面ACD,∴∠BDA为直线BD与平面ACD所成角.
设AB=a,∵△ABC为等腰直角三角形,∴BC=
| 2 |
在Rt△BCD中,∵∠CBD=30°,∴BD=
2
| ||
| 3 |
则sin∠BDA=
| a | ||||
|
| ||
| 4 |
∴直线BD与平面ACD所成角的正弦值为
| ||
| 4 |
点评:本题考查了直线和平面垂直的判定和性质,考查了线面角的求法,考查了学生的空间想象和思维能力,是中档题.

练习册系列答案
相关题目
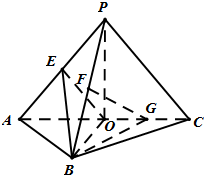 如图,△PAC与△ABC是均以AC为斜边的等腰直角三角形,AC=4,E,F,O分别为PA,PB,AC的中点,G为OC的中点,且PO⊥平面ABC.
如图,△PAC与△ABC是均以AC为斜边的等腰直角三角形,AC=4,E,F,O分别为PA,PB,AC的中点,G为OC的中点,且PO⊥平面ABC. [选做题]
[选做题] 如图,△ABC和△A1AC是正三角形,平面A1AC⊥底面ABC,A1B1⊥∥AB,A1B1=AB=2,
如图,△ABC和△A1AC是正三角形,平面A1AC⊥底面ABC,A1B1⊥∥AB,A1B1=AB=2,