题目内容
如图,在平面直角坐标系xOy中,椭圆C的中心在坐标原点O,右焦点为F.若C的右准线l的方程为x=4,离心率e=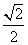 .
.
(1) 求椭圆C的标准方程;
(2) 设点P为准线l上一动点,且在x轴上方.圆M经过O、F、P三点,求当圆心M到x轴的距离最小时圆M的方程.
解:(1) 由题意,设椭圆C的标准方程为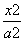 +
+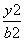 =1(a>b>0),则
=1(a>b>0),则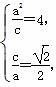 解得a=2
解得a=2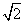 ,c=2.从而b2=a2-c2=4.所以所求椭圆C的标准方程为
,c=2.从而b2=a2-c2=4.所以所求椭圆C的标准方程为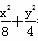 =1.
=1.
(2) (解法1)由(1)知F(2,0).由题意可设P(4,t),t>0.
线段OF的垂直平分线方程为x=1.①
因为线段FP的中点为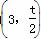 ,斜率为
,斜率为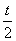 ,
,
所以FP的垂直平分线方程为y-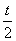 =-
=-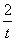 (x-3),即y=-
(x-3),即y=-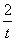 x+
x+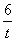 +
+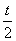 .②
.②
联立①②,解得 .
.
因为t>0,所以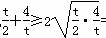 =2
=2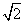 ,当且仅当
,当且仅当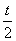 =
=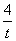 ,即t=2
,即t=2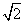 时,圆心M到x轴的距离最小,此时圆心为M(1,2
时,圆心M到x轴的距离最小,此时圆心为M(1,2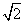 ),半径为OM=3.故所求圆M的方程为(x-1)2+(y-2
),半径为OM=3.故所求圆M的方程为(x-1)2+(y-2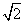 )2=9.
)2=9.
(解法2)由(1)知F(2,0).由题意可设P(4,t),t>0.因为圆M过原点O,故可设圆M的方程为x2+y2+Dx+Ey=0.将点F、P的坐标代入得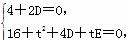 解得
解得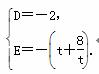
所以圆心M的坐标为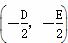 ,即(1,
,即(1,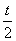 +
+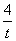 ).因为t>0,所以
).因为t>0,所以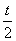 +
+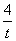 ≥2
≥2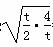 =2
=2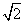 ,当且仅当
,当且仅当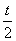 =
=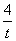 ,即t=2
,即t=2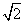 时,圆心M到x轴的距离最小,此时E=-4
时,圆心M到x轴的距离最小,此时E=-4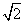 .故所求圆M的方程为x2+y2-2x-4
.故所求圆M的方程为x2+y2-2x-4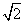 y=0.
y=0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 且
且 ,则实数
,则实数 的取值范围是 .
的取值范围是 .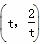 (t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点.
(t∈R,t≠0)为圆心的圆与x轴交于点O、A,与y轴交于点O、B,其中O为原点. 在(0,1)内有极小值,则实数b的取值范围是
在(0,1)内有极小值,则实数b的取值范围是 ) C.(0,+∞) D.(
) C.(0,+∞) D.( ∞,1)
∞,1) ,那么b=
,那么b= B.
B.  C.
C.  D.
D. 
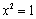 ”是“
”是“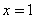 ”的充分不必要条件
”的充分不必要条件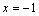 ”是“
”是“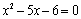 ”的必要不充分条件.
”的必要不充分条件.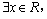 使得
使得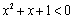 ”的否定是:“
”的否定是:“ 均有
均有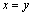 ,则
,则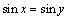 ”的逆否命题为真命题.
”的逆否命题为真命题.