题目内容
如图：是一几何体的三视图，则其体积为3π
3π
．分析：根据已知中的三视图，我们可得该几何体是一个下部是一个底面直径为2，高为2的圆柱，上部是一个底面直径为2，高为3的圆锥的组合体，代入圆锥体积和圆柱体积公式，可得答案．
解答：解：由已知中的三视图，我们可得该几何体是一个组合体
下部是一个底面直径为2，高为2的圆柱，
上部是一个底面直径为2，高为3的圆锥，
∵V柱=π•12•2=2π，V锥=
•π•12•3=π
故该几何体的体积V=V柱+V锥=2π+π=3π
故答案为：3π
下部是一个底面直径为2，高为2的圆柱，
上部是一个底面直径为2，高为3的圆锥，
∵V柱=π•12•2=2π，V锥=
| 1 |
| 3 |
故该几何体的体积V=V柱+V锥=2π+π=3π
故答案为：3π
点评：本题考查的知识点是由三视图求体积，其中分析出几何体的形状及底面直径高等几何量是解答的关键．
练习册系列答案
相关题目
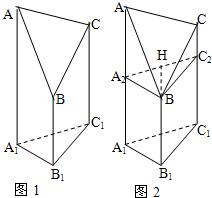如图1是一个直三棱柱（以A1B1C1为底面）被一平面所截得到的几何体，截面为ABC．已知A1B1=B1C1=1，∠A1B1C1=90°，AA1=4，BB1=2，．求此几何体的体积．
已知一几何体的三视图如图，正视图和侧视图都是矩形，俯视图为正方形，在该几何体上任意选择5个顶点，它们可能是如下各种几何形体的5个顶点，这些几何形体是（写出所有正确结论的编号）
已知一几何体的三视图如图，主视图和左视图都是矩形，俯视图为正方形，在该几何体上任意选择4个顶点，以这4个点为顶点的几何形体可能是（ ）
（2010•潍坊三模）如图是一几何体的三视图，则这个几何体外接球的表面积等于
B．
C．
D．
