题目内容
设函数![]() .
.
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)若![]() ,且
,且![]() 在区间
在区间![]() 内存在极值,求整数
内存在极值,求整数![]() 的值.
的值.
解:(Ⅰ)由已知![]() .…………………………(1分)
.…………………………(1分)
当![]() 时,
时,![]() 函数
函数![]() 在
在![]() 内单调递增;………(2分)
内单调递增;………(2分)
当![]() 时,由
时,由![]() 得
得![]() ∴
∴![]() ;……………(3分)
;……………(3分)
由![]() 得
得![]() ∴
∴![]() .……………………(4分)
.……………………(4分)
∴![]() 在
在![]() 内单调递增,在
内单调递增,在![]() 内单调递减.…………(5分)
内单调递减.…………(5分)
(Ⅱ)当![]() 时,
时,![]()
∴![]() ………………………………………(6分)
………………………………………(6分)
令![]() ,
,
则![]() ∴
∴![]() 在
在![]() 内单调递减.……………………(8分)
内单调递减.……………………(8分)
∵![]()
![]()
![]() …………………………(9分)
…………………………(9分)
∴![]() 即
即![]() 在(3,4)内有零点,即
在(3,4)内有零点,即![]() 在(3,4)内存在极值.
在(3,4)内存在极值.
…………………………………(11分)
又∵![]() 在
在![]() 上存在极值,且
上存在极值,且![]() ,∴k=3
,∴k=3

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目









 ,
, 的值;
的值; 的最小值。
的最小值。 )
)
 上是单调函数,求
上是单调函数,求 的取值范围。
的取值范围。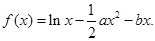
 时,求
时,求 的最大值;
的最大值; ,(
,( ),其图象上任意一点
),其图象上任意一点 处切线的斜率
处切线的斜率 ≤
≤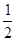 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,
, 的最小正周期以及单调增区间;
的最小正周期以及单调增区间; 时,求
时,求 ,求
,求 的值.
的值. 。
。 的单调区间;
的单调区间; ,不等式
,不等式 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;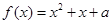 在区间[0, 2] 恰有两个不等实根,求a的取值范围。
在区间[0, 2] 恰有两个不等实根,求a的取值范围。