题目内容
下列集合A到集合B的对应中,
①A=N,B=Z,对应法则f:x→y=-x,x∈A,y∈B.
②A=R+,B=R+,f:x→y=![]() ,x∈A,y∈B.
,x∈A,y∈B.
③A={α|0°≤α≤90°},B={x|0≤x≤1},对应法则f:取正弦.
④A=N*,B={0,1},对应法则f:除以2得的余数.
⑤A={-4,-1,1,4},B={-2,-1,1,2},对应法则f:x→y=|x|2,x∈A,y∈B.
⑥A={平面内边长不同的等边三角形},B={平面内半径不同的圆},对应法则f:作等边三角形的内切圆.
其中是A到B的映射的有________,是A到B的一一映射的有________.
答案:①②③④⑥,②③⑥
提示:
提示:
|
首先读懂各对应中的法则的含义,再依据映射、一一映射概念判断. |

练习册系列答案
相关题目

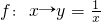 ,x∈A,y∈B.
,x∈A,y∈B.