题目内容
平面上有四点A、B、Q、P,其中A、B为定点,且|AB|=
,P、Q为动点,满足|AP|=|PQ|=|QB|=1,△APB和△PQB的面积分别为m、n.
(1)求∠A=30°,求∠Q
(2) 求m2+n2的最大值.
| 3 |
(1)求∠A=30°,求∠Q
(2) 求m2+n2的最大值.
(1)由余弦定理得PB2=1+3-2
cosA,PB2=1+1-2cosQ
∴4-2
cosA=2-2cosQ,由A=30°求得cosQ=
∴Q=60
(2)m2+n2=(
×1×
sinA)2+(
×1×1×sinQ)2=
sin2A+
(1-cos2Q)=-
(cosA-
)2+
∴当cosA=
时,m2+n2的最大值为
| 3 |
∴4-2
| 3 |
| 1 |
| 2 |
∴Q=60
(2)m2+n2=(
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 2 |
| ||
| 6 |
| 7 |
| 8 |
∴当cosA=
| ||
| 6 |
| 7 |
| 8 |

练习册系列答案
相关题目
 , P、Q为动点,满足
, P、Q为动点,满足 ,⊿APB和⊿PQB的面积分别为
,⊿APB和⊿PQB的面积分别为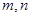 。
。 ,求
,求 (2) 求
(2) 求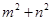 的最大值
的最大值 ,P、Q为动点,满足|AP|=|PQ|=|QB|=1,△APB和△PQB的面积分别为m、n.
,P、Q为动点,满足|AP|=|PQ|=|QB|=1,△APB和△PQB的面积分别为m、n.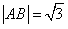 ,P、Q为动点,满足|AP|=|PQ|=|QB|=1,△APB和△PQB的面积分别为m,n。
,P、Q为动点,满足|AP|=|PQ|=|QB|=1,△APB和△PQB的面积分别为m,n。