题目内容
在等比数列{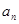 }中,
}中,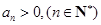 ,公比
,公比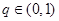 ,且
,且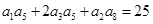 ,
, 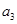 与
与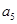 的等比中项为2.
的等比中项为2.
(1)求数列{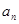 }的通项公式;
}的通项公式;
(2)设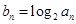 ,数列{
,数列{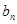 }的前
}的前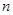 项和为
项和为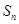 ,当
,当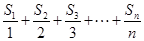 最大时,求
最大时,求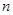 的值。
的值。
【答案】
(1)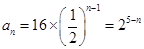
(2)n=8或9
【解析】解:(1)因为a1a5 + 2a3a5 +a 2a8=25,所以,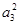 + 2a3a5 +
+ 2a3a5 +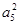 =25
=25
又an>o,…a3+a5=5,…………………………3分
又a3与a5的等比中项为2,所以,a3a5=4
而q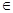 (0,1),所以,a3>a5,所以,a3=4,a5=1,
(0,1),所以,a3>a5,所以,a3=4,a5=1,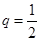 ,a1=16,所以,
,a1=16,所以,
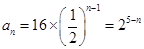 …………………………6分
…………………………6分
(2)bn=log2 an=5-n,所以,bn+1-bn=-1,
所以,{bn}是以4为首项,-1为公差的等差数列。。。。。。。。。8分
所以,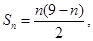
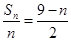 …………………………10分
…………………………10分
所以,当n≤8时,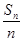 >0,当n=9时,
>0,当n=9时,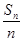 =0,n>9时,
=0,n>9时,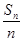 <0,
<0,
当n=8或9时,
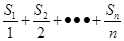 最大。 …………………………13分
最大。 …………………………13分

练习册系列答案
相关题目
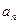 }中,
}中,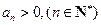 ,公比
,公比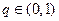 ,且
,且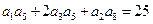 ,
, 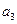 与
与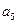 的等比中项为2.
的等比中项为2.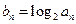 ,数列{
,数列{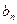 }的前
}的前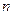 项和为
项和为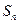 ,当
,当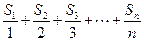 最大时,求
最大时,求 }中,若
}中,若 ,则
,则 的值是 .
的值是 . (
( )中,若
)中,若 ,
, ,则该数列的前10项和为( )
,则该数列的前10项和为( ) B.
B. C.
C. D.
D.