题目内容
【题目】若函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,则称区间
,则称区间![]() 为函数
为函数![]() 的一个“倒值区间”.定义在
的一个“倒值区间”.定义在![]() 上的奇函数
上的奇函数![]() ,当
,当![]() 时,
时,![]()
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)求函数![]() 在
在![]() 上的“倒值区间”;
上的“倒值区间”;
(Ⅲ)记函数![]() 在整个定义域内的“倒值区间”为
在整个定义域内的“倒值区间”为![]() ,设
,设![]() ,则是否存在实数
,则是否存在实数![]() ,使得函数
,使得函数![]() 的图像与函数
的图像与函数![]() 的图像有两个不同的交点?若存在,求出
的图像有两个不同的交点?若存在,求出![]() 的值;若不存在,试说明理由.
的值;若不存在,试说明理由.
【答案】(Ⅰ)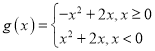 ; (Ⅱ)
; (Ⅱ)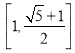 ;(Ⅲ)
;(Ⅲ)![]()
【解析】
(Ⅰ)当![]() ,利用函数奇偶性可知
,利用函数奇偶性可知![]() ,代入求得
,代入求得![]() 时的解析式,从而得到分段函数解析式;(Ⅱ)设
时的解析式,从而得到分段函数解析式;(Ⅱ)设![]() ,利用
,利用![]() 单调性和“倒值区间”的定义可得
单调性和“倒值区间”的定义可得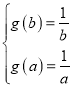 ,解方程求得结果;(Ⅲ)当
,解方程求得结果;(Ⅲ)当![]() 时,
时,![]() ,不满足
,不满足![]() 在
在![]() 上的值域,可知
上的值域,可知![]() 在
在![]() 上的“倒值区间”为
上的“倒值区间”为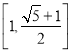 ,同理可得
,同理可得![]() 在
在![]() 上的“倒值区间”;根据
上的“倒值区间”;根据![]() 解析式可得到交点位置,根据交点位置可得关于
解析式可得到交点位置,根据交点位置可得关于![]() 的方程,利用函数值域可求得
的方程,利用函数值域可求得![]() 的范围;通过两段范围可确定
的范围;通过两段范围可确定![]() 的取值.
的取值.
(Ⅰ)当![]() 时,
时,![]()
![]() 为奇函数
为奇函数
![]()
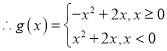
(Ⅱ)设![]() ,由(Ⅰ)知,
,由(Ⅰ)知,![]() 在
在![]() 上单调递减
上单调递减
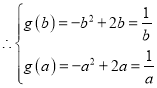 ,整理得:
,整理得: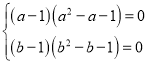
解得: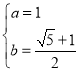
![]() 函数
函数![]() 在
在![]() 上的“倒值区间”为:
上的“倒值区间”为: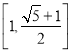
(Ⅲ)由(Ⅱ)知,函数![]() 在
在![]() 上的“倒值区间”为
上的“倒值区间”为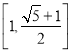
当倒值区间![]() 时,
时,![]()
而函数![]() 在
在![]() 上的值域为
上的值域为![]()
![]() 函数
函数![]() 在
在![]() 上不存在倒值区间
上不存在倒值区间
即:函数![]() 在
在![]() 上的“倒值区间”为
上的“倒值区间”为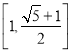
当![]() 时,同理可求得
时,同理可求得![]() 的倒值区间为
的倒值区间为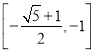
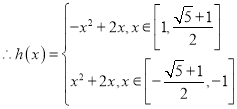
若函数![]() 的图像与
的图像与![]() 的图像有两个不同的交点,则两个交点分别在第一、三象限
的图像有两个不同的交点,则两个交点分别在第一、三象限
当交点在第一象限时,方程![]()
即:![]() 在区间
在区间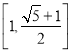 内恰有一个解
内恰有一个解
当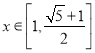 ,
,![]() 单调递减且
单调递减且![]()
![]()
当交点在第三象限时,方程![]()
即:![]() 在区间
在区间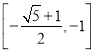 内恰有一个解
内恰有一个解
![]()
综上可得:![]()

【题目】某大学生参加社会实践活动,对某公司1月份至6月份销售某种配件的销售量及销售单价进行了调查,销售单价x和销售量y之间的一组数据如下表所示:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售单价(元) | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
销售量(件) | 11 | 10 | 8 | 6 | 5 | 14.2 |
(1)根据1至5月份的数据,求出y关于x的回归直线方程;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5元,则认为所得到的回归直线方程是理想的,试问(1)中所得到的回归直线方程是否理想?
(3)预计在今后的销售中,销售量与销售单价仍然服从(1)中的关系,若该种机器配件的成本是2.5元/件,那么该配件的销售单价应定为多少元才能获得最大利润?(注:利润=销售收入-成本).
参考公式:回归直线方程![]() ,其中
,其中![]() ,
,![]()
【题目】某舆情机构为了解人们对某事件的关注度,随机抽取了![]() 人进行调查,其中女性中对该事件关注的占
人进行调查,其中女性中对该事件关注的占![]() ,而男性有
,而男性有![]() 人表示对该事件没有关注.
人表示对该事件没有关注.
关注 | 没关注 | 合计 | |
男 |
| ||
女 | |||
合计 |
(1)根据以上数据补全![]() 列联表;
列联表;
(2)能否有![]() 的把握认为“对事件是否关注与性别有关”?
的把握认为“对事件是否关注与性别有关”?
(3)已知在被调查的女性中有![]() 名大学生,这其中有
名大学生,这其中有![]() 名对此事关注.现在从这
名对此事关注.现在从这![]() 名女大学生中随机抽取
名女大学生中随机抽取![]() 人,求至少有
人,求至少有![]() 人对此事关注的概率.
人对此事关注的概率.
附表:
|
|
|
|
|
|
|
|
|
|
|
|
![]()
