题目内容
(2013•汕头二模)在△ABC中,内角A,B,C对应的边分别是a,b,c,已知c=2,C=
,△ABC的面积S△ABC=
,则△ABC的周长为( )
| π |
| 3 |
| 3 |
分析:根据△ABC的面积求得 ab=4,再由余弦定理求得 a2+b2=8,由此求得a+b的值,再由c的值,即可得到△ABC的周长.
解答:解:在△ABC中,∵△ABC的面积S△ABC=
=
ab•sinC=
ab•
,∴ab=4.
再由余弦定理 c2=4=a2+b2-2ab•cosC=a2+b2-4,∴a2+b2=8,
∴a+b=
=
=4,
故△ABC的周长为 a+b+c=4+2=6,
故选A.
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
再由余弦定理 c2=4=a2+b2-2ab•cosC=a2+b2-4,∴a2+b2=8,
∴a+b=
| (a+b)2 |
| a2+b2+2ab |
故△ABC的周长为 a+b+c=4+2=6,
故选A.
点评:本题主要考查三角形的面积公式、余弦定理的应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2013•汕头二模)执行框图,若输出结果为
(2013•汕头二模)执行框图,若输出结果为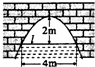 (2013•汕头二模)如图是抛物线形拱桥,当水面在l时,拱顶离水面2米,水面宽4米,水位下降2米后水面宽
(2013•汕头二模)如图是抛物线形拱桥,当水面在l时,拱顶离水面2米,水面宽4米,水位下降2米后水面宽