题目内容
13.已知函数f(x)=ln(ex+1)+ax,(x∈R)是偶函数,且在区间[0,+∞)上是增函数.(1)试确定实数a的值;
(2)先判断函数f(x)在区间(-∞,0]上的单调性,并用定义证明你的结论;
(3)关于x的不等式f(x)≥b-ln$\frac{1}{2}$在R上恒成立,求实数b的取值范围.
分析 (1)根据f(x)是R上的偶函数,f(-x)=f(x)对任意实数x恒成立,列出方程求出a的值;
(2)f(x)在区间(-∞,0]上是减函数,利用定义证明即可;
(3)由不等式f(x)≥b-ln$\frac{1}{2}$在R上恒成立,求出f(x)在R上的最小值,即可得出b的取值范围.
解答 解:(1)∵函数f(x)=ln(ex+1)+ax是R上的偶函数,
即f(-x)=ln(e-x+1)-ax=f(x),
∴ln(ex+1)+ax-(ln(e-x+1)-ax)=0对任意实数x恒成立,
∴ln$\frac{{e}^{x}+1}{{e}^{-x}+1}$+2ax=0对任意实数x恒成立;
又$\frac{{e}^{x}+1}{{e}^{-x}+1}$=ex,上式变成ln(ex)+2ax=(2a+1)x=0对任意实数x恒成立,
∴a=-$\frac{1}{2}$;
(2)∵f(x)=ln(ex+1)-$\frac{1}{2}$x是偶函数,且在区间[0,+∞)上是增函数,
∴f(x)在区间(-∞,0]上是减函数;
用定义证明如下:任取x1、x2∈(-∞,0],且x1<x2;
则-x1>-x2≥0,
∴f(-x1)>f(-x2),
又∵f(x)是R上的偶函数,
∴f(-x1)=f(x1),f(-x2)=f(x2);
∴f(x1)>f(x2),
∴f(x)在区间(-∞,0]上是减函数;
(3)∵关于x的不等式f(x)≥b-ln$\frac{1}{2}$在R上恒成立,
∴ln(ex+1)-$\frac{1}{2}$x≥b-ln$\frac{1}{2}$,
∴b≤ln(ex+1)-$\frac{1}{2}$x+ln$\frac{1}{2}$,
又∵f(x)=ln(ex+1)-$\frac{1}{2}$x是R上的偶函数,
且在(-∞,0]上是减函数,在[0,+∞)上是增函数,
∴x=0时f(x)取得最小值ln(e0+1)-$\frac{1}{2}$×0=ln2,
∴b≤ln2+ln$\frac{1}{2}$=ln(2×$\frac{1}{2}$)=0,
即实数b的取值范围是b≤0.
点评 本题考查了函数的奇偶性的应用问题,也考查了利用函数的单调性求最值的应用问题,考查了转化思想,是综合性题目.

| A. | $\frac{(2n-1){3}^{n}+5}{2}$ | B. | $\frac{(2n-3){3}^{n}+5}{2}$ | C. | $\frac{(2n-5){3}^{n}+5}{2}$ | D. | $\frac{(2n+5){3}^{n}+5}{2}$ |
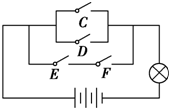 一个电路如图所示,C、D、E、F为4个开关,其闭合的概率都是$\frac{1}{2}$,且是相互独立的,则灯亮的概率是( )
一个电路如图所示,C、D、E、F为4个开关,其闭合的概率都是$\frac{1}{2}$,且是相互独立的,则灯亮的概率是( )| A. | $\frac{9}{16}$ | B. | $\frac{7}{16}$ | C. | $\frac{13}{16}$ | D. | $\frac{3}{16}$ |