题目内容
某电器商经过多年的经验发现本店每个月售出的电冰箱的台数ξ是一个随机变量,它的分布列为:P(ξ=i)= (i=1,2,…,12);设每售出一台电冰箱,电器商获利300元.如销售不出,则每台每月需花保管费100元.问电器商每月初购进多少台电冰箱才能使月平均收益最大?
(i=1,2,…,12);设每售出一台电冰箱,电器商获利300元.如销售不出,则每台每月需花保管费100元.问电器商每月初购进多少台电冰箱才能使月平均收益最大?
解:设x为电器商每月初购进的冰箱的台数,依题意,只需考虑1≤x≤12的情况.
设电器商每月的收益为y
则y是随机变量ξ的函数,且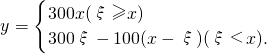
于是电器商每月获益的平均数,即为数学期望
Ey=300x(Px+Px+1+…+P12)+[300-100(x-1)]P1+[2×300-100(x-2)]P2+…+[(x-1)×300-100]Px-1
=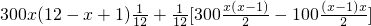 =
=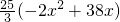 .
.
∵x∈N*,
∴当x=9或x=10时,数学期望最大.
分析:根据题意设出变量,设x为电器商每月初购进的冰箱的台数,依题意,只需考虑1≤x≤12的情况.设电器商每月的收益为y,列出关于x与y之间的关系式,写出电器商每月获益的数学期望,整理出最简结果,根据二次函数的性质,求出结论.
点评:本题考查离散型随机变量的期望,考查二次函数的性质,是一个综合题目,这种题目是概率同函数结合的问题,一般比较困难,解题时注意自变量的取值范围.
设电器商每月的收益为y
则y是随机变量ξ的函数,且
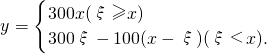
于是电器商每月获益的平均数,即为数学期望
Ey=300x(Px+Px+1+…+P12)+[300-100(x-1)]P1+[2×300-100(x-2)]P2+…+[(x-1)×300-100]Px-1
=
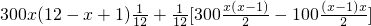 =
=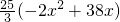 .
.∵x∈N*,
∴当x=9或x=10时,数学期望最大.
分析:根据题意设出变量,设x为电器商每月初购进的冰箱的台数,依题意,只需考虑1≤x≤12的情况.设电器商每月的收益为y,列出关于x与y之间的关系式,写出电器商每月获益的数学期望,整理出最简结果,根据二次函数的性质,求出结论.
点评:本题考查离散型随机变量的期望,考查二次函数的性质,是一个综合题目,这种题目是概率同函数结合的问题,一般比较困难,解题时注意自变量的取值范围.

练习册系列答案
相关题目
某校共有学生2000名,各年级男、女生人数如右表.已知在全校学生中随机抽取1名,抽到二年级女生的可能性0.19.现用分层抽样的方法在全校抽取64名学生,则应在三年级抽取的学生人数为________.
| 一年级 | 二年级 | 三年级 | |
| 女生 | 373 | C2 | C1 |
| 男生 | 377 | 370 | C2 |

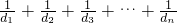 4(n∈N*)5,求Tn;
4(n∈N*)5,求Tn; ,
, ,v>0,则(u-v)2+(
,v>0,则(u-v)2+(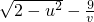 )2的最小值为
)2的最小值为
 .若某人获得两个“支持”,则给予10万元的创业资助;若只获得一个“支持”,则给予5万元的资助;若未获得“支持”,则不予资助,令ξ表示该公司的资助总额.求出ξ数学期望Eξ.
.若某人获得两个“支持”,则给予10万元的创业资助;若只获得一个“支持”,则给予5万元的资助;若未获得“支持”,则不予资助,令ξ表示该公司的资助总额.求出ξ数学期望Eξ.