题目内容

函数f（x）满足f（x）•f（x+2）=13，若f（0）=2，则f（2010）=

A.
13
B.
2
C.
$数学公式$
D.
$数学公式$

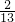
C
分析：根据f（x）•f（x+2）=13可知f（x+4）=f（x），即f（x）是以4为周期的函数，又因为2010=502×4+2，所以f（2010）=f（2），进而可得答案．
解答：∵ $\text{[math]}$ ，∴f（x+4）=f（x）．
∵2010=502×4+2，∴ $\text{[math]}$ ．
故选C．
点评：此题重点考查递推关系下的函数求值；此类题的解决方法一般是求出函数解析式后代值，或者得到函数的周期性求解．

练习册系列答案

课时精练系列答案

课时全练讲练测全程达标系列答案

课时天天练系列答案

课时学案系列答案

课堂达标100分系列答案

课堂过关循环练系列答案

课堂检测10分钟系列答案

课堂练习系列答案

课堂练习检测系列答案

课堂作业四点导学学案精编系列答案

相关题目

（2013•菏泽二模）已知定义在R上的奇函数f（x）满足f（x+2e）=-f（x）（其中e=2.7182…），且在区间[e，2e]上是减函数．令a=

，则（　　）

A．f（a）＜f（b）＜f（c）

B．f（b）＜f（c）＜f（a）

C．f（c）＜f（a）＜f（b）

D．f（c）＜f（b）＜f（a）

已知定义域为R的函数f（x）满足f（-x）=-f（x+4），则x＞2时，f（x）单调递增，若x₁+x₂＜4，且（x₁-2）（x₂-2）＜0，则f（x₁）+f（x₂）与0的大小关系是（）
A．f（x₁）+f（x₂）＞0
B．f（x₁）+f（x₂）=0
C．f（x₁）+f（x₂）＜0
D．f（x₁）+f（x₂）≤0

已知定义域为R的函数f（x）满足f（-x）=-f（x+4），则x＞2时，f（x）单调递增，若x₁+x₂＜4，且（x₁-2）（x₂-2）＜0，则f（x₁）+f（x₂）与0的大小关系是（）
A．f（x₁）+f（x₂）＞0
B．f（x₁）+f（x₂）=0
C．f（x₁）+f（x₂）＜0
D．f（x₁）+f（x₂）≤0

已知定义域为R的函数f（x）满足f（-x）=-f（x+4），则x＞2时，f（x）单调递增，若x₁+x₂＜4，且（x₁-2）（x₂-2）＜0，则f（x₁）+f（x₂）与0的大小关系是（）
A．f（x₁）+f（x₂）＞0
B．f（x₁）+f（x₂）=0
C．f（x₁）+f（x₂）＜0
D．f（x₁）+f（x₂）≤0

已知定义在R上的奇函数f（x）满足f（x+2e）=-f（x）（其中e=2.7182…），且在区间[e，2e]上是减函数．令a=

，则（）
A．f（a）＜f（b）＜f（c）
B．f（b）＜f（c）＜f（a）
C．f（c）＜f（a）＜f（b）
D．f（c）＜f（b）＜f（a）