题目内容
设函数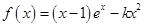 (其中
(其中 ).
).
(Ⅰ)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅱ)当 时,求函数
时,求函数 在
在 上的最大值
上的最大值 .
.
【答案】
(Ⅰ)函数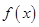 的递减区间为
的递减区间为 ,递增区间为
,递增区间为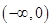 ,
,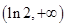 .
.
(Ⅱ)函数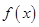 在
在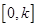 上的最大值
上的最大值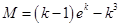 .
.
【解析】
试题分析:(Ⅰ)通过“求导数、求驻点、讨论导数的正负、确定函数的单调区间”,本题利用“表解法”,直观,易于理解.
(Ⅱ)求函数的最值,通过“求导数、求驻点、讨论导数的正负、确定函数的极值、比较区间端点函数值”等步骤,不断地构造函数加以转化,是解答本题的关键.
试题解析:
(Ⅰ)当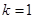 时,
时,
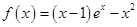 ,
,
令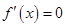 ,得
,得 ,
,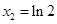 2分
2分
当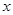 变化时,
变化时,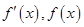 的变化如下表:
的变化如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
极大值 |
|
极小值 |
|
右表可知,函数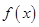 的递减区间为
的递减区间为 ,递增区间为
,递增区间为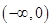 ,
,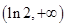 .
.
6分
(Ⅱ) ,
,
令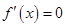 ,得
,得 ,
,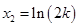 ,
7分
,
7分
令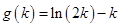 ,则
,则 ,所以
,所以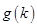 在
在 上递增,
上递增,
所以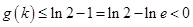 ,从而
,从而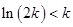 ,所以
,所以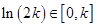
所以当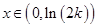 时,
时,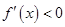 ;当
;当 时,
时,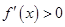 ;
;
所以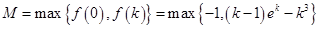 10分
10分
令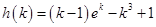 ,则
,则 ,
,
令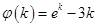 ,则
,则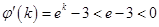
所以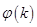 在
在 上递减,而
上递减,而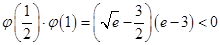
所以存在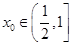 使得
使得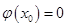 ,且当
,且当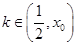 时,
时,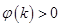 , 12分
, 12分
当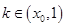 时,
时, ,
,
所以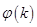 在
在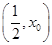 上单调递增,在
上单调递增,在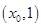 上单调递减.
上单调递减.
因为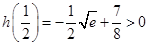 ,
, ,
,
所以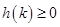 在
在 上恒成立,当且仅当
上恒成立,当且仅当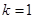 时取得“
时取得“ ”.
”.
综上,函数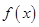 在
在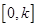 上的最大值
上的最大值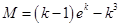 .
14分
.
14分
考点:应用导数研究函数的单调性、极值、最值

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
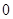
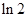


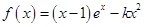 (其中
(其中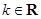 ).
).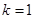 时,求函数
时,求函数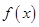 的单调区间和极值;
的单调区间和极值;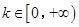 时,函数
时,函数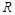 上有且只有一个零点.
上有且只有一个零点.
 其中
其中
 的单调区间;
的单调区间;
 其中
其中
 的单调区间;
的单调区间;