题目内容
过点P(1,0)作曲线C:y=x2(x∈(0,+∞)的切线,切点为M1,设M1在x轴上的投影是点P1.又过点P1作曲线C的切线,切点为M2,设M2在x轴上的投影是点P2,….依此下去,得到一系列点M1,M2…,Mn,…,设它们的横坐标a1,a2,…,an,…,构成数列为{an}.
(1)求证数列{an}是等比数列,并求其通项公式;
(2)令bn=
,求数列{bn}的前n项和Sn.
(1)求证数列{an}是等比数列,并求其通项公式;
(2)令bn=
| n |
| an |
(1)对y=x2求导数,得y'=2x,切点是Mn(an,an2)的切线方程是y-an2=2an(x-an).(2分)
当n=1时,切线过点P(1,0),即0-a12=2a1(1-a1),得a1=2;
当n>1时,切线过点Pn-1(an-1,0),即0-
=2an(an-1-an),得
=2
所以数列{an}是首项a1=2,公比为2的等比数列.
所以数列{an}的通项公式为an=2n,n∈N*(6分)
(2)∵bn=
,an=2n,∴bn=
Sn=
+
+
+…+
①
2Sn=
+
+…+
+
②
①-②,得-Sn=
+
+
+…+
-
=
-
=1-
-
=1-
当n=1时,切线过点P(1,0),即0-a12=2a1(1-a1),得a1=2;
当n>1时,切线过点Pn-1(an-1,0),即0-
| a | 2n |
| an |
| an-1 |
所以数列{an}是首项a1=2,公比为2的等比数列.
所以数列{an}的通项公式为an=2n,n∈N*(6分)
(2)∵bn=
| n |
| an |
| n |
| 2n |
Sn=
| 1 |
| 21 |
| 2 |
| 22 |
| 3 |
| 23 |
| n |
| 2n |
2Sn=
| 1 |
| 22 |
| 2 |
| 23 |
| n-1 |
| 2n |
| n |
| 2n+1 |
①-②,得-Sn=
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| n |
| 2n+1 |
| ||||
1-
|
| n |
| 2n+1 |
| 1 |
| 2n |
| n |
| 2n+1 |
| 3 |
| 2n+1 |

练习册系列答案
相关题目

 (2009•锦州一模)过点P(1,0)作曲线C:y=x2(x>0)的切线,切点为Q1,没Q1在x轴上的投影是P1,又过P1,作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2…,依次下去,得到一系列点Q1Q2,…Qn,设Qn的横坐标为an.
(2009•锦州一模)过点P(1,0)作曲线C:y=x2(x>0)的切线,切点为Q1,没Q1在x轴上的投影是P1,又过P1,作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2…,依次下去,得到一系列点Q1Q2,…Qn,设Qn的横坐标为an.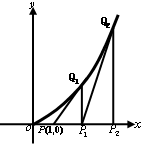 (2013•韶关二模)如图,过点P(1,0)作曲线C:y=x2(x∈(0,+∞))的切线,切点为Q1,设点Q1在x轴上的投影是点P1;又过点P1作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2;…;依此下去,得到一系列点Q1,Q2,Q3-Qn,设点Qn的横坐标为an.
(2013•韶关二模)如图,过点P(1,0)作曲线C:y=x2(x∈(0,+∞))的切线,切点为Q1,设点Q1在x轴上的投影是点P1;又过点P1作曲线C的切线,切点为Q2,设Q2在x轴上的投影是P2;…;依此下去,得到一系列点Q1,Q2,Q3-Qn,设点Qn的横坐标为an.