题目内容
已知对任意实数x,二次函数f(x)=ax2+bx+c恒非负,且a<b,则M=| a+b+c | b-a |
分析:从二次函数的二次项系数及判别式限制,得到a,b,c满足的不等关系;将M中的c利用得到的不等关系去掉;将代数式变形;利用基本不等式求出最小值,注意检验等号何时取到.
解答:解:∵二次函数f(x)=ax2+bx+c恒非负
所以a>0 且 b2-4ac≤0
所以 4ac≥b2
所以 c≥
∴M=
≥
=
=
≥
=3
当且仅当3a=b-a且c=
即c=b=4a时,取等号
故答案为3
所以a>0 且 b2-4ac≤0
所以 4ac≥b2
所以 c≥
| b2 |
| 4a |
∴M=
| a+b+c |
| b-a |
a+b+
| ||
| b-a |
| (2a+b)2 |
| 4a(b-a) |
| [3a+(b-a)]2 |
| 4a(b-a) |
| 4(b-a)×3a |
| 4a(b-a) |
当且仅当3a=b-a且c=
| b2 |
| 4a |
故答案为3
点评:本题考查二次函数的函数值的情况取决于二次项系数的符号及判别式的符号、考查不等式的性质、考查利用基本不等式求函数的最值,关键是凑出能与分母有联系的形式,要注意使用时满足的条件:一正、二定、三相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
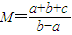 的最小值是 .
的最小值是 .