题目内容
函数y=sin22x+2cosx2的导数是______.
由复合函数的导数公式得到
y′=2sin2x•(sin2x)′-2sinx2•(x2)′
=4sin2xcos2x-4xsinx2
=2sin4x-4xsinx2
故答案为2sin4x-4xsinx2
y′=2sin2x•(sin2x)′-2sinx2•(x2)′
=4sin2xcos2x-4xsinx2
=2sin4x-4xsinx2
故答案为2sin4x-4xsinx2

练习册系列答案
相关题目
函数y=sin22x是( )
| A、周期为π的奇函数 | ||
| B、周期为π的偶函数 | ||
C、周期为
| ||
D、周期为
|
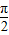 的奇函数
的奇函数 的偶函数
的偶函数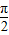 的奇函数
的奇函数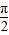 的偶函数
的偶函数