题目内容
(本小题满分l4分)已知数列 的前n项和为
的前n项和为 ,正数数列
,正数数列 中
中
(e为自然对数的底 )且
)且 总有
总有 是
是 与
与 的等差中项,
的等差中项, 的等比中项.
的等比中项.
(1) 求证:  有
有 ;
;
(2) 求证: 有
有 .
.
【答案】
解:(1)  是
是 与
与 的等差中项
的等差中项




(2)由(1)得

 6分
6分
 的等比中项
的等比中项




综上所述,总有 成立
14分
成立
14分
解法二:



(2)

 的等比中项
的等比中项

ii)假设 时不等式
时不等式 成立,
成立,
则n=k+1时要证明
只需证明:
即只需证明: ….9分
….9分
 ……..10分
……..10分
 只需证明
只需证明
只需证明 13分
13分
由 可知上面结论都成立
可知上面结论都成立
综合(i)(ii)可知 ,
,  成立 …..14分
成立 …..14分
法三:
n=1时同法一: 时左边证明同法一
10分
时左边证明同法一
10分
当 时,证明右边如下:
时,证明右边如下:

只需证明 11分
11分
 只需证明
只需证明
 只需证明
只需证明 13分
13分
由 可知上面结论都成立
可知上面结论都成立
综上所述 ,
,
 成立 …..14分
成立 …..14分
注1: 必须
必须 才行
才行

实际上



练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的前
的前 项和为
项和为 ,且
,且 ,
, (
( )
) ,证明:
,证明: .
. 的正方体
的正方体 中,
中, 是
是 的中点,
的中点, 在线段
在线段 上,且
上,且 .
. 与
与 所成角的余弦值;
所成角的余弦值; 面
面 ;
; 到面
到面
 中,底面
中,底面 是矩形,
是矩形, 平面
平面 ,
, ,
,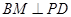 于点
于点 .
.
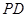 ;
; 与平面
与平面 所成的角的余弦值.
所成的角的余弦值.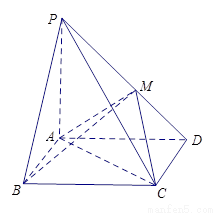
 有唯一的零点
有唯一的零点 .
.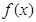 的表达式;
的表达式; 上具有单调性,求实数
上具有单调性,求实数 的取值范围;
的取值范围; (其中
(其中 )的图象如下图所示。
)的图象如下图所示。
 ,
, 及
及 的值;
的值;
 ,且
,且 ,求
,求 的值.。
的值.。