题目内容
6.在平面直角坐标系xOy中,P为不等式组$\left\{\begin{array}{l}2x-y+2≥0\\ x-2y+1≤0\\ x+y-2≤0\end{array}\right.$,所表示的区域上的一个动点,已知点Q(1,-1),那么|PQ|的最大值为( )| A. | $\sqrt{5}$ | B. | $\sqrt{10}$ | C. | 2 | D. | 2$\sqrt{3}$ |
分析 作出不等式度对应的平面区域,利用两点间的距离关系进行求解,即可得到结论.
解答 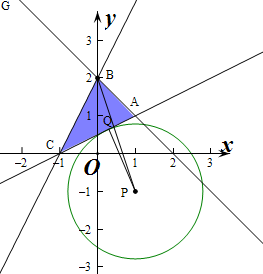 解:作出不等式组对应的平面区域如图:
解:作出不等式组对应的平面区域如图:
由$\left\{\begin{array}{l}{2x-y+2=0}\\{x+y-2=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=0}\\{y=2}\end{array}\right.$,
则B(0,2),
∴由图象可知当P位于B,|PQ|的距离最大,
最大为$\sqrt{(1-0)^{2}+(-1-2)^{2}}=\sqrt{1+9}=\sqrt{10}$.
故选:B.
点评 本题主要考查线性规划的应用,利用数形结合,以及两点间的距离公式是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(b>a>0)的两条渐近线的夹角为60°,则双曲线的离心率为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\frac{4}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
 一个四棱锥的底面是正方形,其正视图和侧视图均为如图所示的等腰三角形,则该四棱锥的侧面积为16$\sqrt{5}$.
一个四棱锥的底面是正方形,其正视图和侧视图均为如图所示的等腰三角形,则该四棱锥的侧面积为16$\sqrt{5}$. 的图象关于( )
的图象关于( )  对称 C.
对称 C. 轴对称 D.直线
轴对称 D.直线 对称
对称