题目内容
11．已知函数f（x）=$\left\{\begin{array}{l}{x-5，x≥6}\\{f（x+2），x＜6}\end{array}\right.$则f（5）等于（ ）| A． | 2 | B． | 3 | C． | 4 | D． | -2 |
分析 首先由5＜6得到f（5）=f（7），再由7＞6，得到f（7）=75-，得到答案．
解答 解：由已知函数f（x）=$\left\{\begin{array}{l}{x-5，x≥6}\\{f（x+2），x＜6}\end{array}\right.$则f（5）=f（5+2）=f（7）=7-5=2．
故选：A．
点评 本题考查了分段函数的函数值求法；关键是明确自变量范围，对号入座，代入对应的解析式求值．
练习册系列答案
相关题目
1．若cos（α-β）cosβ-sin（α-β）sinβ=-m，且α为第三象限，则sinα的值（ ）
| A． | -$\sqrt{1-{m}^{2}}$ | B． | $\sqrt{1-{m}^{2}}$ | C． | $\sqrt{{m}^{2}-1}$ | D． | -$\sqrt{{m}^{2}-1}$ |
如图，函数y=f（x）是可导函数，曲线y=f（x）过点（2，3），且在x=2处的切线l在y轴上的截距为2，令g（x）=xf（x），则曲线y=g（x）在x=2处的切线方程是4x-y-2=0．
3．对于函数y=f（x），当x∈（0，+∞）时，总有f（x）＜xf′（x），若m＞n＞0，则下列不等式中，恒成立的是（ ）
| A． | $\frac{f（m）}{n}$＜$\frac{f（n）}{m}$ | B． | $\frac{f（m）}{m}$＜$\frac{f（n）}{n}$ | C． | $\frac{f（m）}{n}$＞$\frac{3f（n）}{m}$ | D． | $\frac{f（m）}{m}$＞$\frac{f（n）}{n}$ |
5．甲有三本不同的书，乙去借阅，且至少借1本，则不同借法的总数为（ ）
| A． | 3 | B． | 6 | C． | 7 | D． | 9 |
6．如图⊙O中，弦AB与弦CD相交于点P，∠B=38°，∠APD=80°，则∠A等于（ ）
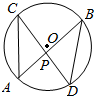
| A． | 38° | B． | 42° | C． | 80° | D． | 118° |