题目内容
8.已知各项均不为零的数列{an},定义向量$\overrightarrow{c_n}=({{a_n},{a_{n+1}}}),\overrightarrow{b_n}=({2n+2,-2n}),n∈{N^*}$.下列命题中真命题是( )| A. | 若?n∈N*总有cn⊥bn成立,则数列{an}是等比数列 | |
| B. | 若?n∈N*总有cn∥bn成立成立,则数列{an}是等比数列 | |
| C. | 若?n∈N*总有cn⊥bn成立,则数列{an}是等差数列 | |
| D. | 若?n∈N*总有cn∥bn成立,则数列{an}是等差数列 |
分析 根据题意,分析平面向量平行、垂直的坐标表示,判断数列{an}是否为等差或等比数列.
解答 解:若cn∥bn成立,则-2nan=(2n+2)an+1,即-nan=(n+1)an+1,即$\frac{{a}_{n+1}}{{a}_{n}}$=-$\frac{n}{n+1}$,
∴an=$\frac{{a}_{n}}{{a}_{n-1}}$•$\frac{{a}_{n-1}}{{a}_{n-2}}$…$\frac{{a}_{2}}{{a}_{1}}$•a1=(-$\frac{n-1}{n}$)•(-$\frac{n-2}{n-1}$)•…•(-$\frac{1}{2}$)•a1=$\frac{1}{n}$(-1)n-1a1,
∴数列{an}既不是等差数列,也不是等比数列,
∴B,D错误,
若?n∈N*总有cn⊥bn成立,则(2n+2)an-2nan+1=0,nan=(n+1)an+1,即$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{n+1}{n}$,
∴an=$\frac{{a}_{n}}{{a}_{n-1}}$•$\frac{{a}_{n-1}}{{a}_{n-2}}$…$\frac{{a}_{2}}{{a}_{1}}$•a1=$\frac{n}{n-1}$•$\frac{n-1}{n-2}$•…•2•a1=na1,
∴数列{an}是等差数列,
∴A错误,C正确,
故选:C
点评 本题考查了平面向量平行的坐标表示,也考查了等差与等比数列的应用问题,中档题目.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
9.执行如图所示的程序框图,则输出s的值为( )


| A. | $\sqrt{2018}-1$ | B. | $\sqrt{2017}-1$ | C. | $\sqrt{2016}-1$ | D. | $\sqrt{2015}-1$ |
16.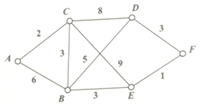 某市A,B,C,D,E,F六个城区欲架设光缆,如图所示,两点之间的线段及线段上的相应数字分别对应城区可以架设光缆及所需光缆的长度,如果任意两个城市之间均匀光缆相通,则所需光缆的总长度的最小值是( )
某市A,B,C,D,E,F六个城区欲架设光缆,如图所示,两点之间的线段及线段上的相应数字分别对应城区可以架设光缆及所需光缆的长度,如果任意两个城市之间均匀光缆相通,则所需光缆的总长度的最小值是( )
 某市A,B,C,D,E,F六个城区欲架设光缆,如图所示,两点之间的线段及线段上的相应数字分别对应城区可以架设光缆及所需光缆的长度,如果任意两个城市之间均匀光缆相通,则所需光缆的总长度的最小值是( )
某市A,B,C,D,E,F六个城区欲架设光缆,如图所示,两点之间的线段及线段上的相应数字分别对应城区可以架设光缆及所需光缆的长度,如果任意两个城市之间均匀光缆相通,则所需光缆的总长度的最小值是( )| A. | 10 | B. | 12 | C. | 14 | D. | 15 |
13.若函数f(x)=$\frac{1}{2}{x^2}$+lnx-ax+1在区间($\frac{1}{2}$,3)上单调递减,则实数a的取值范围为( )
| A. | (-∞,2] | B. | (-∞,2) | C. | [3,+∞) | D. | $(-∞,\frac{5}{2})$ |
20.设(1+i)(x+yi)=2,其中x,y实数,则|x+2yi|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
17.据统计,2016年“双11”天猫总成交金额突破3万亿元.某购物网站为优化营销策略,对11月11日当天在该网站进行网购消费且消费金额不超过1000元的1000名网购者(其中有女性800名,男性200名)进行抽样分析.采用根据性别分层抽样的方法从这1000名网购者中抽取100名进行分析,得到下表:(消费金额单位:元)
女性和男性消费情况如表
(Ⅰ)计算x,y的值;在抽出的100名且消费金额在[800,1000](单位:元)的网购者中随机选出两名发放网购红包,求选出的两名网购者恰好是一男一女的概率;
(Ⅱ)若消费金额不低于600元的网购者为“网购达人”,低于600元的网购者为“非网购达人”,根据以上统计数据填写右边2×2列联表,并回答能否有99%以上的把握认为“是否为‘网购达人’与性别有关?”
附:(${Χ^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
女性和男性消费情况如表
| 消费金额 | (0,200) | [200,400) | [400,600) | [600,800) | [800,1000] |
| 女性人数 | 5 | 10 | 15 | 47 | x |
| 男性人数 | 2 | 3 | 10 | y | 2 |
| 女性 | 男性 | 总计 | |
| 网购达人 | |||
| 非网购达人 | |||
| 总计 |
| P(Χ2>k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |