题目内容
19.当k$∈(-\frac{1}{2},0)$时,方程$\sqrt{|1-x|}$=-kx的解的个数是3.分析 方程$\sqrt{|1-x|}$=-kx的解的个数,即为函数y=$\sqrt{|1-x|}$和函数y=-kx的图象的交点个数,当x>1时,y=$\sqrt{x-1}$,联立直线y=-kx,运用判别式为0,求得k,结合图象的交点个数,即可得到解的个数.
解答 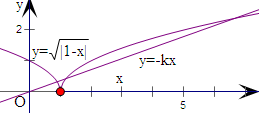 解:方程$\sqrt{|1-x|}$=-kx的解的个数,即为
解:方程$\sqrt{|1-x|}$=-kx的解的个数,即为
函数y=$\sqrt{|1-x|}$和函数y=-kx的图象的交点个数,
当x>1时,y=$\sqrt{x-1}$,联立直线y=-kx,
平方可得k2x2-x+1=0,由判别式为0,即1-4k2=0,
可得k=±$\frac{1}{2}$(舍去正的),
由右边的图象,可得-$\frac{1}{2}<k<0$,
即为0<-k<$\frac{1}{2}$,可得直线y=-kx和y=$\sqrt{|1-x|}$有三个交点.
即方程的解的个数为3.
故答案为:3.
点评 本题考查函数和方程的转化思想的运用,考查数形结合的思想方法的运用,属于中档题.

练习册系列答案
相关题目
10.在数列{an}中,若存在一个确定的正整数T,对任意n∈N*满足an+T=an,则称{an}是周期数列,T叫做它的周期.已知数列{xn}满足x1=1,x2=a(a≤1),xn+2=|xn+1-xn|,若数列{xn}的周期为3,则{xn}的前2014项的和为( )
| A. | 1344 | B. | 1343 | C. | 1224 | D. | 1223 |
7. 如图所示的算法流程图中,若f(x)=lnx,g(x)=log2x,则h(4)的值等于( )
如图所示的算法流程图中,若f(x)=lnx,g(x)=log2x,则h(4)的值等于( )
 如图所示的算法流程图中,若f(x)=lnx,g(x)=log2x,则h(4)的值等于( )
如图所示的算法流程图中,若f(x)=lnx,g(x)=log2x,则h(4)的值等于( )| A. | 1 | B. | -1 | C. | 2 | D. | ln4 |
14.若|$\overrightarrow{e}$|=1,且$\overrightarrow{a}⊥\overrightarrow{e}$,|$\overrightarrow{a}$|=2,则|4$\overrightarrow{a}-\overrightarrow{e}$|=( )
| A. | $\sqrt{37}$ | B. | $\sqrt{65}$ | C. | 8 | D. | $\sqrt{13}$ |
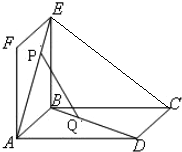 如图:已知有公共边AB的两个全等的矩形ABCD和ABEF不在同一个平面内,P,Q分别是对角线AE,BD上的点,且AP=DQ,求证:PQ∥面CBE.
如图:已知有公共边AB的两个全等的矩形ABCD和ABEF不在同一个平面内,P,Q分别是对角线AE,BD上的点,且AP=DQ,求证:PQ∥面CBE.