题目内容
已知函数 是
是 上的偶函数,对任意
上的偶函数,对任意 ,都有
,都有 成立,当
成立,当 且
且 时,都有
时,都有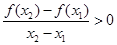 给出下列命题:
给出下列命题:
① 且
且 是函数
是函数 的一个周期;②直线
的一个周期;②直线 是函数
是函数 的一条对称轴;
的一条对称轴;
③函数 在
在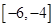 上是增函数; ④函数
上是增函数; ④函数 在
在 上有四个零点.其中正确命题的序号为 (把所有正确命题的序号都填上)
上有四个零点.其中正确命题的序号为 (把所有正确命题的序号都填上)
【答案】
(1)(2)(4)
【解析】
试题分析:∵对任意 ,都有
,都有 成立
成立
当 ,可得
,可得 ,
,
又∵函数 是
是 上的偶函数
上的偶函数
∴ ,
,
又由当 且
且 时,都有
时,都有 ,
,
∴函数在区间 单调递增
单调递增
故函数 的简图如下图所示:
的简图如下图所示:

由图可知:(1)正确,(2)正确,(3)错误,(4)正确
故答案:(1)(2)(4)
考点:命题的真假判断与应用;偶函数;函数奇偶性的性质.
点评:本题考查的知识点是函数的图象,函数的奇偶性,函数的周期性,函数的零点,解答的关键是根据已知,判断函数的性质,并画出函数的草图,结合草图分析题目中相关结论的正误.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 是
是 上的偶函数,满足
上的偶函数,满足 ,当
,当 时,
时, ,则( )
,则( ) B.
B.
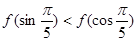 D.
D.
 是
是 上的偶函数,且
上的偶函数,且 在
在 上是减函数,若
上是减函数,若 ,则
,则 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 是
是 上的偶函数,对任意
上的偶函数,对任意 ,都有
,都有 成立,
成立, 且
且 时,都有
时,都有 给出下列命题:
给出下列命题: 且
且 是函数
是函数 的一个周期;
的一个周期; 是函数
是函数 上是增函数;
上是增函数; 上有四个零点.
上有四个零点.