题目内容
等比数列{an}中的前n项和为Sn,若
=5,则
=
| S10 |
| S5 |
| S20 |
| S10 |
17
17
.分析:由题意可知公比q≠1,由求和公式代入已知可得q5=4,而所求的式子化简后可得1+q10,代入可求.
解答:解:设等比数列{an}的公比为q,由题意可知q≠1,
则
=
=1+q5=5,可得q5=4,
故
=
=
=1+q10=1+42=17
故答案为:17
则
| S10 |
| S5 |
| ||
|
| 1-q10 |
| 1-q5 |
故
| S20 |
| S10 |
| ||
|
| 1-q20 |
| 1-q10 |
故答案为:17
点评:本题考查等比数列的性质和求和公式,整体代入是解决问题的关键,属中档题.

练习册系列答案
相关题目
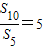 ,则
,则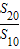 = .
= .