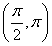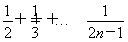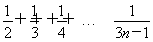题目内容
若实数x、y、m满足|x－m|＞|y－m|，则称x比y远离m.
(1)若x2－1比1远离0，求x的取值范围；
(2)对任意两个不相等的正数a、b，证明：a3＋b3比a2b＋ab2远离2ab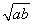
.
（1）x∈(－∞，－
)∪(
，＋∞)．（2）见解析
【解析】(1)【解析】
x∈(－∞，－)∪(，＋∞)．
(2)证明：对任意两个不相等的正数a、b，有
a3＋b3>2ab
，a2b＋ab2>2ab
.
因为|a3＋b3－2ab
|－|a2b＋ab2－2ab
|＝(a＋b)(a－b)2>0，所以|a3＋b3－2ab
|>|a2b＋ab2－2ab
|，即a3＋b3比a2b＋ab2远离2ab
.
练习册系列答案
相关题目
