题目内容
20.某人在一山坡P处观看对面山项上的一座铁塔,如图所示,塔高BC=80(米),塔所在的山高OB=220(米),OA=200(米),图中所示的山坡可视为直线l且点P在直线l上,![]() 与水平地面的夹角为
与水平地面的夹角为![]() ,tan
,tan![]() =
=![]() 试问,此人距水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)?
试问,此人距水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)?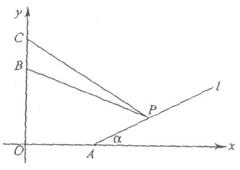
20. 解:如图所示,建立平面直角坐标系,则A(200,0),
B(0,220),C(0,300)。 直线l的方程为y=(x-200) tan
直线l的方程为y=(x-200) tan![]() , 即
, 即
y=![]()
设点P的坐标为(x, y),则 P(x, ![]() )(x>200).
)(x>200).
由经过两点的直线的斜率 公式
kPC=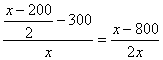 ,
,
kPB=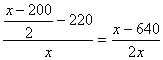
由直线PC到直线PB的角的公式得
tan ![]() BPC=
BPC=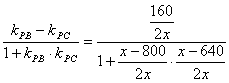
=![]()
=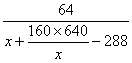 (x>200)
(x>200)
要使tan![]() BPC达到最大,只须x+
BPC达到最大,只须x+![]() 达到最小、由均值不等式
达到最小、由均值不等式
![]() ≥2
≥2![]() -288,
-288,
当且仅当x=![]() 时上式取得等号,故当x=320时 tan
时上式取得等号,故当x=320时 tan ![]() BPC最大,这时,点P的纵坐标y为
BPC最大,这时,点P的纵坐标y为
y=![]() =60.
=60.
由此实际问题知,0<∠BPC<![]() ,所以tan
,所以tan![]() BPC最大时,∠BPC最大,故当此人距水平地面
BPC最大时,∠BPC最大,故当此人距水平地面

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
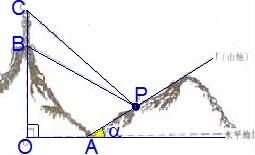 某人在一山坡P处观看对面山项上的一座铁塔,如图所示,塔及所在的山崖可视为图中的竖线OC,塔高BC?80(米),山高OB?220(米),OA?200(米),图中所示的山坡可视为直线l且点P在直线l上,l与水平地面的夹角为α,tanα=
某人在一山坡P处观看对面山项上的一座铁塔,如图所示,塔及所在的山崖可视为图中的竖线OC,塔高BC?80(米),山高OB?220(米),OA?200(米),图中所示的山坡可视为直线l且点P在直线l上,l与水平地面的夹角为α,tanα= 某人在一山坡P处观看对面山顶上的一座铁塔,如图所示,塔高BC=40(米),塔所在的山高OB=290(米),OA=210(米),图中所示的山坡可视为直线l且点P在直线l上,l与水平地面的夹角为α,
某人在一山坡P处观看对面山顶上的一座铁塔,如图所示,塔高BC=40(米),塔所在的山高OB=290(米),OA=210(米),图中所示的山坡可视为直线l且点P在直线l上,l与水平地面的夹角为α, .试问此人距水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高).
.试问此人距水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高).
 .试问,此人距山崖的水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)?
.试问,此人距山崖的水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)?
 .试问,此人距山崖的水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)?
.试问,此人距山崖的水平地面多高时,观看塔的视角∠BPC最大(不计此人的身高)?