题目内容
11、若b1=1,对于任何n∈N*,都有bn>0,且nbn+12-2bn2-(2n-1)bn+1bn=0,设M(x)表示整数x的个位数字,则M(b2010)=
2
.分析:对所给的代数式进行整理得到两个因式的积的形式,得到数列是一个bn+1=2bn种关系,协会粗第2010项的表示式,对于指数形式进行整理,得到结果.
解答:解:nbn+12-2bn2-(2n-1)bn+1bn=0,
(nbn+1+bn)(bn+1-2bn)=0
∵bn>0,bn+1>0 则 nbn+1+bn 大于0
有 b n+1-2bn=0
bn+1=2bn
则bn=2 (n-1) b1=2(n-1)
b2010=2 2009={(210 )10}10×29=(1024 10)10×512
个位数为2(4 10)10=2(2 10) 20=2×1024 20
个位数为 4 20 ×2=(210)4×2=10244×2
个位数为 4×4×2=32
个位数为 2
故答案为:2
(nbn+1+bn)(bn+1-2bn)=0
∵bn>0,bn+1>0 则 nbn+1+bn 大于0
有 b n+1-2bn=0
bn+1=2bn
则bn=2 (n-1) b1=2(n-1)
b2010=2 2009={(210 )10}10×29=(1024 10)10×512
个位数为2(4 10)10=2(2 10) 20=2×1024 20
个位数为 4 20 ×2=(210)4×2=10244×2
个位数为 4×4×2=32
个位数为 2
故答案为:2
点评:本题考查函数与数列的综合题目,本题解题的关键是看出数列的特点,针对于所给的数列的特点写出数列的表示式,整理出结果.

练习册系列答案
相关题目
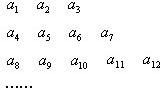 将数列{an}中的所有项按第一行排3项,以下每一行比上一行多一项的规则排成如下数表:
将数列{an}中的所有项按第一行排3项,以下每一行比上一行多一项的规则排成如下数表: ,求上表中第k(k∈N*)行所有项的和s(k).
,求上表中第k(k∈N*)行所有项的和s(k).