题目内容
已知椭圆 过点P(3,1),其左、右焦点分别为F1,F2,且
过点P(3,1),其左、右焦点分别为F1,F2,且 ,则椭圆E的离心率是 .
,则椭圆E的离心率是 .
【答案】分析:设椭圆的左右焦点分别为F1(-c,0),F2(c,0),其中c= ,根据
,根据 建立关于c的方程,解之得c=4.然后根据椭圆经过点P(3,1),结合
建立关于c的方程,解之得c=4.然后根据椭圆经过点P(3,1),结合 ,解关于a、b的方程组,可得a=3
,解关于a、b的方程组,可得a=3 ,b=
,b= ,从而得到椭圆的离心率.
,从而得到椭圆的离心率.
解答:解:设椭圆 的左右焦点分别为F1(-c,0),F2(c,0),其中c=
的左右焦点分别为F1(-c,0),F2(c,0),其中c=
∴ =(3+c,1),
=(3+c,1), =(3-c,1),
=(3-c,1),
∴ ,解之得c=4(舍负)
,解之得c=4(舍负)
又∵椭圆 过点P(3,1),
过点P(3,1),
∴ 且
且 ,解之得a=3
,解之得a=3 ,b=
,b=
因此椭圆的离心率为e= =
=
故答案为:
点评:本题给出椭圆上一个定点坐标,在已知向量数量积的情况下求椭圆的离心率,着重考查了向量数量积的坐标运算和椭圆的基本概念和简单几何性质等知识点,属于中档题.
 ,根据
,根据 建立关于c的方程,解之得c=4.然后根据椭圆经过点P(3,1),结合
建立关于c的方程,解之得c=4.然后根据椭圆经过点P(3,1),结合 ,解关于a、b的方程组,可得a=3
,解关于a、b的方程组,可得a=3 ,b=
,b= ,从而得到椭圆的离心率.
,从而得到椭圆的离心率.解答:解:设椭圆
 的左右焦点分别为F1(-c,0),F2(c,0),其中c=
的左右焦点分别为F1(-c,0),F2(c,0),其中c=
∴
 =(3+c,1),
=(3+c,1), =(3-c,1),
=(3-c,1),∴
 ,解之得c=4(舍负)
,解之得c=4(舍负)又∵椭圆
 过点P(3,1),
过点P(3,1),∴
 且
且 ,解之得a=3
,解之得a=3 ,b=
,b=
因此椭圆的离心率为e=
 =
=
故答案为:

点评:本题给出椭圆上一个定点坐标,在已知向量数量积的情况下求椭圆的离心率,着重考查了向量数量积的坐标运算和椭圆的基本概念和简单几何性质等知识点,属于中档题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
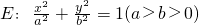 过点P(3,1),其左、右焦点分别为F1,F2,且
过点P(3,1),其左、右焦点分别为F1,F2,且 ,则椭圆E的离心率是________.
,则椭圆E的离心率是________. ),Q(2,
),Q(2, ).
).