题目内容
已知函数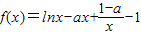 (a∈R).
(a∈R).(Ⅰ)当
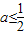 时,讨论f(x)的单调性;
时,讨论f(x)的单调性;(Ⅱ)设g(x)=x2-2bx+4.当
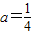 时,若对任意x1∈(0,2),存在x2∈[1,2],使f(x1)≥g(x2),求实数b取值范围.
时,若对任意x1∈(0,2),存在x2∈[1,2],使f(x1)≥g(x2),求实数b取值范围.
【答案】分析:(Ⅰ)直接利用函数与导数的关系,求出函数的导数,再讨论函数的单调性;
(Ⅱ)利用导数求出f(x)的最小值、利用二次函数知识或分离常数法求出g(x)在闭区间[1,2]上的最大值,然后解不等式求参数.
解答:解:(Ⅰ)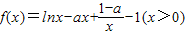 ,
,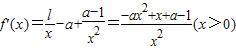
令h(x)=ax2-x+1-a(x>0)
(1)当a=0时,h(x)=-x+1(x>0),
当x∈(0,1),h(x)>0,f′(x)<0,函数f(x)单调递减;
当x∈(1,+∞),h(x)<0,f′(x)>0,函数f(x)单调递增.
(2)当a≠0时,由f′(x)=0,即ax2-x+1-a=0,解得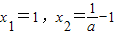 .
.
当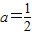 时x1=x2,h(x)≥0恒成立,此时f′(x)≤0,函数f(x)单调递减;
时x1=x2,h(x)≥0恒成立,此时f′(x)≤0,函数f(x)单调递减;
当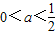 时,
时,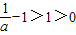 ,x∈(0,1)时h(x)>0,f′(x)<0,函数f(x)单调递减;
,x∈(0,1)时h(x)>0,f′(x)<0,函数f(x)单调递减;
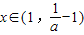 时,h(x)<0,f′(x)>0,函数f(x)单调递增;
时,h(x)<0,f′(x)>0,函数f(x)单调递增;
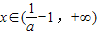 时,h(x)>0,f′(x)<0,函数f(x)单调递减.
时,h(x)>0,f′(x)<0,函数f(x)单调递减.
当a<0时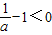 ,当x∈(0,1),h(x)>0,f′(x)<0,函数f(x)单调递减;
,当x∈(0,1),h(x)>0,f′(x)<0,函数f(x)单调递减;
当x∈(1,+∞),h(x)<0,f′(x)>0,函数f(x)单调递增.
综上所述:当a≤0时,函数f(x)在(0,1)单调递减,(1,+∞)单调递增;
当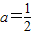 时x1=x2,h(x)≥0恒成立,此时f′(x)≤0,函数f(x)在(0,+∞)单调递减;
时x1=x2,h(x)≥0恒成立,此时f′(x)≤0,函数f(x)在(0,+∞)单调递减;
当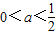 时,函数f(x)在(0,1)单调递减,
时,函数f(x)在(0,1)单调递减,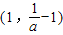 单调递增,
单调递增,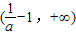 单调递减.
单调递减.
(Ⅱ)当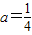 时,f(x)在(0,1)上是减函数,在(1,2)上是增函数,所以对任意x1∈(0,2),
时,f(x)在(0,1)上是减函数,在(1,2)上是增函数,所以对任意x1∈(0,2),
有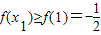 ,
,
又已知存在x2∈[1,2],使f(x1)≥g(x2),所以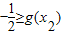 ,x2∈[1,2],(※)
,x2∈[1,2],(※)
又g(x)=(x-b)2+4-b2,x∈[1,2]
当b<1时,g(x)min=g(1)=5-2b>0与(※)矛盾;
当b∈[1,2]时,g(x)min=g(b)=4-b2≥0也与(※)矛盾;
当b>2时,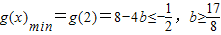 .
.
综上,实数b的取值范围是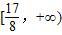 .
.
点评:本题将导数、二次函数、不等式知识有机的结合在一起,考查了利用导数研究函数的单调性、利用导数求函数的最值以及二次函数的最值问题,考查了同学们分类讨论的数学思想以及解不等式的能力;考查了学生综合运用所学知识分析问题、解决问题的能力.
(Ⅱ)利用导数求出f(x)的最小值、利用二次函数知识或分离常数法求出g(x)在闭区间[1,2]上的最大值,然后解不等式求参数.
解答:解:(Ⅰ)
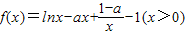 ,
,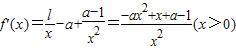
令h(x)=ax2-x+1-a(x>0)
(1)当a=0时,h(x)=-x+1(x>0),
当x∈(0,1),h(x)>0,f′(x)<0,函数f(x)单调递减;
当x∈(1,+∞),h(x)<0,f′(x)>0,函数f(x)单调递增.
(2)当a≠0时,由f′(x)=0,即ax2-x+1-a=0,解得
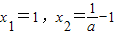 .
.当
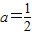 时x1=x2,h(x)≥0恒成立,此时f′(x)≤0,函数f(x)单调递减;
时x1=x2,h(x)≥0恒成立,此时f′(x)≤0,函数f(x)单调递减;当
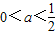 时,
时,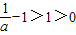 ,x∈(0,1)时h(x)>0,f′(x)<0,函数f(x)单调递减;
,x∈(0,1)时h(x)>0,f′(x)<0,函数f(x)单调递减;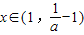 时,h(x)<0,f′(x)>0,函数f(x)单调递增;
时,h(x)<0,f′(x)>0,函数f(x)单调递增;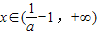 时,h(x)>0,f′(x)<0,函数f(x)单调递减.
时,h(x)>0,f′(x)<0,函数f(x)单调递减.当a<0时
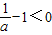 ,当x∈(0,1),h(x)>0,f′(x)<0,函数f(x)单调递减;
,当x∈(0,1),h(x)>0,f′(x)<0,函数f(x)单调递减;当x∈(1,+∞),h(x)<0,f′(x)>0,函数f(x)单调递增.
综上所述:当a≤0时,函数f(x)在(0,1)单调递减,(1,+∞)单调递增;
当
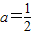 时x1=x2,h(x)≥0恒成立,此时f′(x)≤0,函数f(x)在(0,+∞)单调递减;
时x1=x2,h(x)≥0恒成立,此时f′(x)≤0,函数f(x)在(0,+∞)单调递减;当
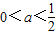 时,函数f(x)在(0,1)单调递减,
时,函数f(x)在(0,1)单调递减,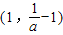 单调递增,
单调递增,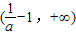 单调递减.
单调递减.(Ⅱ)当
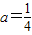 时,f(x)在(0,1)上是减函数,在(1,2)上是增函数,所以对任意x1∈(0,2),
时,f(x)在(0,1)上是减函数,在(1,2)上是增函数,所以对任意x1∈(0,2),有
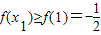 ,
,又已知存在x2∈[1,2],使f(x1)≥g(x2),所以
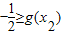 ,x2∈[1,2],(※)
,x2∈[1,2],(※)又g(x)=(x-b)2+4-b2,x∈[1,2]
当b<1时,g(x)min=g(1)=5-2b>0与(※)矛盾;
当b∈[1,2]时,g(x)min=g(b)=4-b2≥0也与(※)矛盾;
当b>2时,
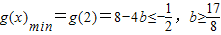 .
.综上,实数b的取值范围是
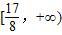 .
.点评:本题将导数、二次函数、不等式知识有机的结合在一起,考查了利用导数研究函数的单调性、利用导数求函数的最值以及二次函数的最值问题,考查了同学们分类讨论的数学思想以及解不等式的能力;考查了学生综合运用所学知识分析问题、解决问题的能力.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 (a∈R且a≠0).
(a∈R且a≠0).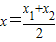 ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. (a∈R且a≠0).
(a∈R且a≠0). ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. (a∈R且a≠0).
(a∈R且a≠0). ;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”.
;②曲线C在M处的切线平行于直线AB,则称函数F(x)存在“中值相依切线”. ,a∈R.
,a∈R. 上的任意一个x,都有f(x)≤1成立,求a的取值范围.
上的任意一个x,都有f(x)≤1成立,求a的取值范围. (a∈R).
(a∈R). 在[1,e]上是增函数,求a的取值范围;
在[1,e]上是增函数,求a的取值范围;
 .
.