题目内容
(三级达标校与非达标校做)
已知函数f(x)=2x+
(x∈R)
(Ⅰ) 判断函数f(x)的奇偶性,并说明理由;
(Ⅱ)求证f(x)在[0,1]上单调递增,在[-1,0]上单调递减.
已知函数f(x)=2x+
| 1 |
| 2x |
(Ⅰ) 判断函数f(x)的奇偶性,并说明理由;
(Ⅱ)求证f(x)在[0,1]上单调递增,在[-1,0]上单调递减.
(I)证明:函数f(x)为偶函数,证明如下
∵f(-x)=2-x+
=2x+
=f(x)
∴f(x)为偶函数
(II)设0≤x1<x2≤1
则f(x1)-f(x2)=2x1-2x2+
-
=(2x1-2x2)+
=(2x1-2x2)(1-
)
∵0≤x1<x2≤1
∴2x1-2x2<0,
∵2x1•2x2= 2x1+ x2>1
∴1-
>0
即(2x1-2x2)(1-
)<0
∴f(x)在[0,1]上单调递增,
根据偶函数在对称区间上的单调性相反可知函数f(x)在[-1,0]上单调递减.
∵f(-x)=2-x+
| 1 |
| 2-x |
| 1 |
| 2x |
∴f(x)为偶函数
(II)设0≤x1<x2≤1
则f(x1)-f(x2)=2x1-2x2+
| 1 |
| 2x1 |
| 1 |
| 2x2 |
=(2x1-2x2)+
| 2x2-2x1 |
| 2x1•2x2 |
=(2x1-2x2)(1-
| 1 |
| 2x1•2x2 |
∵0≤x1<x2≤1
∴2x1-2x2<0,
∵2x1•2x2= 2x1+ x2>1
∴1-
| 1 |
| 2x1+x2 |
即(2x1-2x2)(1-
| 1 |
| 2x1•2x2 |
∴f(x)在[0,1]上单调递增,
根据偶函数在对称区间上的单调性相反可知函数f(x)在[-1,0]上单调递减.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (三级达标校与非达标校做)
(三级达标校与非达标校做)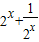 (x∈R)
(x∈R)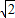 .
.
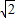 .
.