题目内容
13.已知F为抛物线C:y2=4x的焦点,点E在点C的准线上,且在x轴上方,线段EF的垂直平分线于C的准线交于点Q(-1,$\frac{3}{2}$),与C交于点P,则△PEF的面积为( )| A. | 5 | B. | 10 | C. | 15 | D. | 20 |
分析 由抛物线方程求出焦点坐标,设出E的坐标(-1,m),利用EF和QP垂直求得m的值,则EF、QP的方程可求,求出EF的长度,求出P的坐标,由三角形的面积公式求得△PEF的面积.
解答 解:如图, 由抛物线方程为y2=4x,得F(1,0),设E(-1,m)(m>0),
由抛物线方程为y2=4x,得F(1,0),设E(-1,m)(m>0),
则EF中点为G(0,$\frac{m}{2}$),${k}_{EF}=-\frac{m}{2}$,又Q(-1,$\frac{3}{2}$),
∴${k}_{QG}=\frac{\frac{3}{2}-\frac{m}{2}}{-1-0}=\frac{m-3}{2}$,则$-\frac{m}{2}•\frac{m-3}{2}=-1$,解得:m=4.
∴E(-1,4),
则|EF|=$\sqrt{(-1-1)^{2}+(4-0)^{2}}=2\sqrt{5}$,
直线EF的方程为$\frac{y-0}{4-0}=\frac{x-1}{-1-1}$,化为一般式得:2x+y-2=0.
QG所在直线方程为y-$\frac{3}{2}$=$\frac{1}{2}(x+1)$,即x-2y+4=0.
联立$\left\{\begin{array}{l}{x-2y+4=0}\\{{y}^{2}=4x}\end{array}\right.$,得$\left\{\begin{array}{l}{x=4}\\{y=4}\end{array}\right.$,即P(4,4),
∴P到直线EF的距离为d=$\frac{|2×4+4-2|}{\sqrt{5}}=2\sqrt{5}$.
则△PEF的面积为$\frac{1}{2}×2\sqrt{5}×2\sqrt{5}=10$.
故选:B.
点评 本题考查了抛物线的简单性质,考查了抛物线的应用,平面解析式的基础知识.考查了考生的基础知识的综合运用和知识迁移的能力,是中档题.

| A. | {1,5,6} | B. | {1,4,5,6} | C. | {2,3,4} | D. | {1,6} |
| A. | $\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | $\sqrt{6}$ |

| A. | $\frac{3}{4}$ | B. | $\frac{5}{8}$ | C. | $\frac{7}{8}$ | D. | $\frac{1}{2}$ |
| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{2}{3}π$ | D. | $\frac{4}{3}π$ |
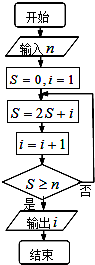
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |