题目内容
如下图，已知点P是圆x2＋y2＝16上的一个动点，点A(12，0)，若线段PA的中点为M，当动点P在圆上运动时，求点M的轨迹方程．
答案：
解析：
解析：
|
分析：由于A是定点，P是定圆上的动点，设出点P的坐标，然后建立与点M的坐标的关系即可求解． 解：设点M的坐标是(x，y)，点P的坐标是(a，b)． 由中点坐标公式，有 所以 又点P(a，b)在圆x2＋y2＝16上， 所以有a2＋b2＝16， 即(2x－12)2＋(2y)2＝16． 整理，得x2＋y2－12x＋32＝0． 所以点M的轨迹方程为x2＋y2－12x＋32＝0． |
练习册系列答案
相关题目
，如下图，已知O为椭圆中心，A1，A2是长轴两端点，太阳位于椭圆的左焦点F处．
(本小题满分12分)
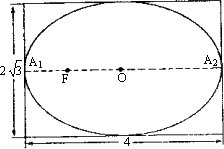
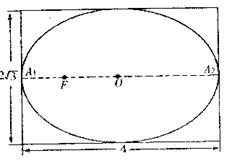
有一幅椭圆型彗星轨道图，长4cm，高
，如下图，
已知O为椭圆中心，A1，A2是长轴两端点，
|
（Ⅰ）建立适当的坐标系，写出椭圆方程，
并求出当彗星运行到太阳正上方时二者在图上的距离；
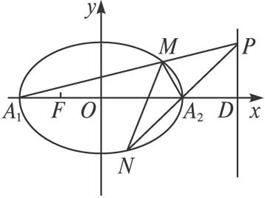
（Ⅱ）直线l垂直于A1A2的延长线于D点，|OD|=4，
设P是l上异于D点的任意一点，直线A1P，A2P分别
交椭圆于M、N（不同于A1，A2）两点，问点A2能否
在以MN为直径的圆上？试说明理由.
cm,如下图,已知O为椭圆中心,A1,A2是长轴两端点,太阳位于椭圆的左焦点F处.