��Ŀ����
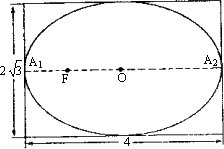
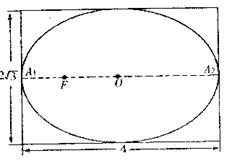
��һ����Բ�����ǹ��ͼ,��4 cm,��2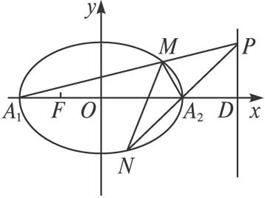
(1)�����ʵ�������ϵ,д����Բ����,��������������е�̫�����Ϸ�ʱ������ͼ�ϵľ���;
(2)ֱ��l��ֱ��A1A2���ӳ�����D��,|OD|=4,��P��l������D�������һ��,ֱ��A1P��A2P�ֱ���Բ��M��N(��ͬ��A1,A2)����,�ʵ�A2�ܷ�����MNΪֱ����Բ�ϣ���˵������.
��:(1)������ͼ��ʾ������ϵ,����Բ����Ϊ![]() +
+![]() =1(a��b��0),������,2a=4,2b=2
=1(a��b��0),������,2a=4,2b=2![]() ,��a=2,b=
,��a=2,b=![]() .��c=1.
.��c=1.

��Բ����Ϊ![]() =1,
=1,
F(-1,0),��x=-1������Բ���̵�y=��![]() ,�൱����λ��̫�����Ϸ�ʱ,������ͼ�еľ���Ϊ1.5 cm.
,�൱����λ��̫�����Ϸ�ʱ,������ͼ�еľ���Ϊ1.5 cm.
(2)��(1)֪,A1(-2,0),A2(2,0),��M(x0,y0),��M����Բ��,��y02=![]() (4-x02),
(4-x02),
�ֵ�M���ڶ���A1,A2,��-2��x0��2.
��P��M��A1���㹲�߿ɵ�P(4,![]() ),
),
��![]() =(x0-2,y0),
=(x0-2,y0),![]() =(2,
=(2,![]() ).
).
��![]() ��
��![]() =2(x0-2)+
=2(x0-2)+![]() =
=![]() (2-x0).
(2-x0).
��2-x0��0.��![]() ��
��![]() ��0.��MA2P���.
��0.��MA2P���.
��P��A2��N���㹲��,��ֱ��A2M��NA2����ֱ.
���A2������MNΪֱ����Բ��.

(��������12��)
��һ����Բ�����ǹ��ͼ����4cm����![]() ������ͼ��
������ͼ��
��֪OΪ��Բ���ģ�A1��A2�dz������˵㣬
|
�������ʵ�������ϵ��д����Բ���̣�
��������������е�̫�����Ϸ�ʱ������ͼ�ϵľ��룻
����ֱ��l��ֱ��A1A2���ӳ�����D�㣬|OD|=4��
��P��l������D�������һ�㣬ֱ��A1P��A2P�ֱ�
����Բ��M��N����ͬ��A1��A2�����㣬�ʵ�A2�ܷ�
����MNΪֱ����Բ�ϣ���˵������.