题目内容
选修4-4:坐标系与参数方程在直角坐标系xOy中,圆
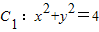 ,圆
,圆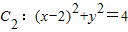
(I)在以圆O为极点,x轴正半轴为极轴的极坐标系中,分别写出圆C1,C2的极坐标方程,并求出圆C1,C2的交点坐标(用坐标表示);
(Ⅱ)求圆C1与C2的公共弦的参数方程.
【答案】分析:(I)利用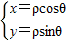 ,以及x2+y2=ρ2,直接写出圆C1,C2的极坐标方程,求出圆C1,C2的交点极坐标,然后求出直角坐标(用坐标表示);
,以及x2+y2=ρ2,直接写出圆C1,C2的极坐标方程,求出圆C1,C2的交点极坐标,然后求出直角坐标(用坐标表示);
(II)解法一:求出两个圆的直角坐标,直接写出圆C1与C2的公共弦的参数方程.
解法二利用直角坐标与极坐标的关系求出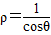 ,然后求出圆C1与C2的公共弦的参数方程.
,然后求出圆C1与C2的公共弦的参数方程.
解答:解:(I)由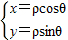 ,x2+y2=ρ2,
,x2+y2=ρ2,
可知圆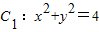 ,的极坐标方程为ρ=2,
,的极坐标方程为ρ=2,
圆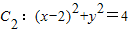 ,即
,即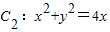 的极坐标方程为ρ=4cosθ,
的极坐标方程为ρ=4cosθ,
解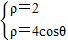 得:ρ=2,
得:ρ=2,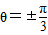 ,
,
故圆C1,C2的交点坐标(2,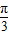 ),(2,
),(2,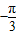 ).
).
(II)解法一:由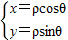 得圆C1,C2的交点的直角坐标(1,
得圆C1,C2的交点的直角坐标(1,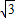 ),(1,
),(1,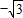 ).
).
故圆C1,C2的公共弦的参数方程为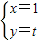
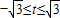
(或圆C1,C2的公共弦的参数方程为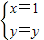
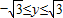 )
)
(解法二)将x=1代入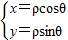 得ρcosθ=1
得ρcosθ=1
从而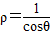 于
于
是圆C1,C2的公共弦的参数方程为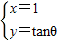
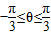 .
.
点评:本题考查简单曲线的极坐标方程,直线的参数方程的求法,极坐标与直角坐标的互化,考查计算能力.
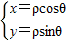 ,以及x2+y2=ρ2,直接写出圆C1,C2的极坐标方程,求出圆C1,C2的交点极坐标,然后求出直角坐标(用坐标表示);
,以及x2+y2=ρ2,直接写出圆C1,C2的极坐标方程,求出圆C1,C2的交点极坐标,然后求出直角坐标(用坐标表示);(II)解法一:求出两个圆的直角坐标,直接写出圆C1与C2的公共弦的参数方程.
解法二利用直角坐标与极坐标的关系求出
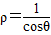 ,然后求出圆C1与C2的公共弦的参数方程.
,然后求出圆C1与C2的公共弦的参数方程.解答:解:(I)由
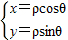 ,x2+y2=ρ2,
,x2+y2=ρ2,可知圆
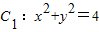 ,的极坐标方程为ρ=2,
,的极坐标方程为ρ=2,圆
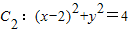 ,即
,即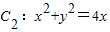 的极坐标方程为ρ=4cosθ,
的极坐标方程为ρ=4cosθ,解
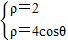 得:ρ=2,
得:ρ=2,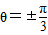 ,
,故圆C1,C2的交点坐标(2,
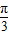 ),(2,
),(2,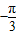 ).
).(II)解法一:由
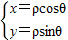 得圆C1,C2的交点的直角坐标(1,
得圆C1,C2的交点的直角坐标(1,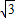 ),(1,
),(1,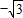 ).
).故圆C1,C2的公共弦的参数方程为
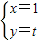
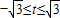
(或圆C1,C2的公共弦的参数方程为
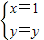
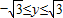 )
)(解法二)将x=1代入
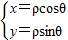 得ρcosθ=1
得ρcosθ=1从而
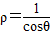 于
于是圆C1,C2的公共弦的参数方程为
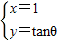
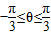 .
.点评:本题考查简单曲线的极坐标方程,直线的参数方程的求法,极坐标与直角坐标的互化,考查计算能力.

练习册系列答案
相关题目
 A.选修4-1:几何证明选讲
A.选修4-1:几何证明选讲