题目内容
已知四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点.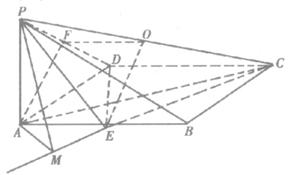
(Ⅰ)求证:AF∥ 平面PEC;
(Ⅱ )求PC与平面ABCD所成角的大小;
(Ⅲ )求二面角P-EC-D的大小.
解法一:(Ⅰ)取PC的中点O,连接OF、OE.

∴FO∥DC,且FO=![]() DC. ∴FO∥AE.
DC. ∴FO∥AE.
又∵E是AB的中点,且AB=DC. ∴FO=AE.
∴四边形AEOF是平行四边形.
∴AF∥OE.
又OE![]() 平面PEC,AF
平面PEC,AF![]() 平面PEC,
平面PEC,
∴AF∥平面PEC.
(Ⅱ)连接AC.∵PA⊥平面ABCD,
∴∠PCA是直线PC与平面ABCD所成的角.
在RtΔPAC中,
tan∠PCA=![]() .
.
即直线PC与平面ABCD所成角的大小为arctan![]() .
.
(Ⅲ)作AM⊥CE,交CE延长线于M,连接PM.
由三垂线定理,得PM⊥CE.
∴∠PMA是二面角P-EC-D的平面角.
由ΔAME∽ΔCBE,可得AM=![]() .
.
∴tan∠PMA=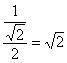 .
.
∴二面角P-EC-D的大小为arctan![]() .
.
解法二:以A为原点,如图建立直角坐标系.
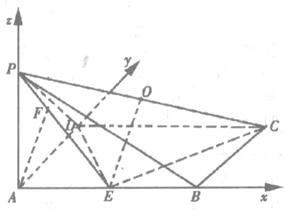
则A(0,0,0),B(2,0,0),C(2,1,0),D(0,1,0),F(0,![]() ,
,![]() ),E(1,0,0),P(0,0,1)
),E(1,0,0),P(0,0,1)
(Ⅰ)取PC的中点O,连接OE.
则O(1,![]() ,
,![]() ).
).
![]() =(0,
=(0,![]() ,
,![]() ),
),![]() =(0,
=(0,![]() ,
,![]() )
)
∴![]() ∥
∥![]() .
.
又OE![]() 平面PEC,AF
平面PEC,AF![]() 平面PEC,
平面PEC,
∴AF∥平面PEC.
(Ⅱ)由题意可得![]() =(2,1,-1),
=(2,1,-1),
平面ABCD的法向量是![]() =(0,0,-1).
=(0,0,-1).
cos<![]() ,
,![]() )=
)=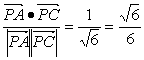
即直线PC与平面ABCD所成角的大小为arcsin![]() .
.
(Ⅲ)设平面PEC的法向量为m=(x,y,z).
![]() =(1,0,-1),
=(1,0,-1),![]() =(1,1,0).
=(1,1,0).
则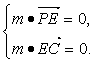 可得
可得![]()
令z=-1,则m=(-1,1,-1).
由(Ⅱ)可得平面ABCD的法向量是![]() (0,0,-1).
(0,0,-1).
cos(m,![]() )=
)=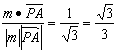
∴二面角P-EC-D的大小为arccos![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知四棱锥P--ABC的底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,e为PC的中点,F为AD的中点.
如图,已知四棱锥P--ABC的底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,e为PC的中点,F为AD的中点. 如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC,侧面PBC⊥底面ABCD,O是BC的中点.
如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC,侧面PBC⊥底面ABCD,O是BC的中点. 已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,E为BC中点,AE与BD交于O点,AB=BC=2CD=2,BD⊥PE.
已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,E为BC中点,AE与BD交于O点,AB=BC=2CD=2,BD⊥PE. 如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠DAB=∠ABC=90°,E是线段PC上一点,PC⊥平面BDE.
如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠DAB=∠ABC=90°,E是线段PC上一点,PC⊥平面BDE.