题目内容
16.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,且离心率e=$\frac{1}{3}$,点P在该椭圆上满足|PF2|=$\frac{8}{3}$c(c为焦半距)(1)是否存在点P,使△PF1F2的边长是由自然数构成的公差为2的等差数列,若存在,求出实数c的值;若不存在,请说明理由;
(2)当c=1时,A是椭圆C的左顶点,且M,N是椭圆C上的两个动点,|$\overrightarrow{AM}$-$\overrightarrow{AN}$|=|$\overrightarrow{AM}$+$\overrightarrow{AN}$|,问直线MN是否过定点?若是,求出定点的坐标,否则说明理由.
分析 (1)求出|PF2|=$\frac{8}{3}$c,|PF1|=$\frac{1}{3}$c,利用△PF1F2的边长是由自然数构成的公差为2的等差数列,可得2c-$\frac{1}{3}$c=$\frac{8}{3}$c-2c=2,无解,即可得出结论.
(2)若|$\overrightarrow{AM}$-$\overrightarrow{AN}$|=|$\overrightarrow{AM}$+$\overrightarrow{AN}$|,则$\overrightarrow{AM}$⊥$\overrightarrow{AN}$,分直线MN斜率存在与不存在讨论,即可求得直线MN过定点(-$\frac{3}{17}$,0).
解答 解:(1)∵离心率e=$\frac{c}{a}$=$\frac{1}{3}$,∴a=3c,b=2$\sqrt{2}$c,
∵|PF2|=$\frac{8}{3}$c,
∴|PF1|=$\frac{10}{3}$c,
∵△PF1F2的边长是由自然数构成的公差为2的等差数列,
∴2c+2=$\frac{8}{3}$c,c=3,
∴存在点P,使△PF1F2的边长是由自然数构成的公差为2的等差数列;
(2)当c=1时,a=3,b=2$\sqrt{2}$,∴椭圆方程为$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{8}$=1.
若|$\overrightarrow{AM}$-$\overrightarrow{AN}$|=|$\overrightarrow{AM}$+$\overrightarrow{AN}$|,则$\overrightarrow{AM}$⊥$\overrightarrow{AN}$.由题意知A(-3,0).
设M(x1,y1),N(x2,y2).
若直线MN斜率不存在,则N(x1,-y1),由$\overrightarrow{AM}$⊥$\overrightarrow{AN}$得(x1+3)(x1+3)-y12=0,
又$\frac{{{x}_{1}}^{2}}{9}+\frac{{{y}_{1}}^{2}}{8}=1$,解得直线MN方程为x=-$\frac{3}{17}$.
若直线MN斜率存在,设方程为y=kx+m,与椭圆方程联立,消去y可得(9k2+8)x2+18kmx+9m2-72=0.
∴x1+x2=-$\frac{18km}{9{k}^{2}+8}$,x1x2=$\frac{9{m}^{2}-72}{9{k}^{2}+8}$.
由$\overrightarrow{AM}$⊥$\overrightarrow{AN}$得(x1+3)(x2+3)+y1y2=0,
整理得(k2+1)x1x2+(km+3)(x1+x2)+m2+9=0
∴(k2+1)×$\frac{9{m}^{2}-72}{9{k}^{2}+8}$+(km+3)×(-$\frac{18km}{9{k}^{2}+8}$)+m2+9=0.
解得m=$\frac{3}{17}$k或m=3k.
若m=3k,即直线MN过定点(-3,0),不合题意舍去.
m=$\frac{3}{17}$k,此时直线过定点(-$\frac{3}{17}$,0)合题意.
斜率不存在时依然满足.
点评 本题考查轨迹方程的求解,考查直线与椭圆的位置关系,考查向量知识的运用,考查分类讨论的数学思想,联立方程,利用韦达定理解题是关键.

| A. | $\frac{3π}{4}$ | B. | $\frac{3π}{8}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{8}$ |
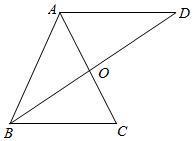 如图,在△ABC中,AB=AC=3,BC=2,B的角平分线交过点A且与BC平行的直线于D,AC与BD交于点O.
如图,在△ABC中,AB=AC=3,BC=2,B的角平分线交过点A且与BC平行的直线于D,AC与BD交于点O.